题目内容
11.(1)计算:-22×|-5$\frac{1}{2}$|-($\frac{1}{3}$-$\frac{1}{2}$)÷(-$\frac{1}{12}$)+1(2)解方程:$\frac{2x-1}{3}=\frac{x+2}{4}-1$
(3)化简求值:已知:多项式-3a-2(3a2b-2a)-3+6a2b-b,其中a=2015,b=2016.
分析 (1)原式先计算乘方及绝对值运算,再计算乘除运算,最后算加减运算即可得到结果;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)原式去括号合并得到最简结果,把a与b的值代入计算即可求出值.
解答 解:(1)原式=-4×$\frac{11}{2}$-(-$\frac{1}{6}$)×(-12)+1=-22-2+1=-23;
(2)去分母,得4(2x-1)=3(x+2)-12
去括号,得8x-4=3x+6-12,
移项及合并同类项,得5x=-2,
系数化为1,得x=-0.4;
(3)原式=-3a-6a2b+4a-3+6a2b-b=a-b-3,
当a=2015,b=2016时,原式=2015-2016-3=-4.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
19.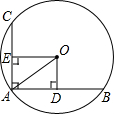 如图,在⊙O中,弦AB⊥AC,OD⊥AB于点D,OE⊥AC于点E,若AB=8cm,AC=6cm,则⊙O的半径OA的长为( )
如图,在⊙O中,弦AB⊥AC,OD⊥AB于点D,OE⊥AC于点E,若AB=8cm,AC=6cm,则⊙O的半径OA的长为( )
 如图,在⊙O中,弦AB⊥AC,OD⊥AB于点D,OE⊥AC于点E,若AB=8cm,AC=6cm,则⊙O的半径OA的长为( )
如图,在⊙O中,弦AB⊥AC,OD⊥AB于点D,OE⊥AC于点E,若AB=8cm,AC=6cm,则⊙O的半径OA的长为( )| A. | 7cm | B. | 6cm | C. | 5cm | D. | 4cm |
20.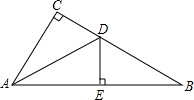 如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )
如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )
 如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )
如图,在直角三角形ABC中,∠C=90°,∠CAB的平分线ADD交BC于点D,若DE垂直平分AB,则下列结论中错误的是( )| A. | AB=2AE | B. | AC=2CD | C. | DB=2CD | D. | AD=2DE |
1.在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
| A. | $sinA=\frac{{\sqrt{3}}}{2}$ | B. | $cosA=\frac{{\sqrt{3}}}{2}$ | C. | $tanA=\frac{1}{2}$ | D. | $cotA=\frac{{\sqrt{3}}}{3}$ |
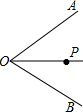 已知点P是∠AOB的角平分线上的一点.
已知点P是∠AOB的角平分线上的一点.