题目内容
1.如图,OA⊥OB,引射线OC(点C在∠AOB外),OD平分∠BOC,OE平分∠AOD.(1)若∠BOC=40°,请依题意补全图,并求∠BOE的度数;
(2)若∠BOC=α(0°<α<180°),请直接写出∠BOE的度数(用含α的代数式表示).
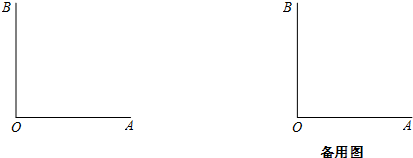
分析 (1)首先根据角平分线的定义求得∠BOD的度数,然后求得∠AOD的度数,根据角平分线的定义求得∠DOE,然后根据∠BOE=∠DOE-∠BOD;
(2)与(1)解法相同.
解答 解:(1)如图,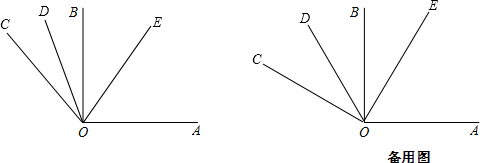 ∵OD是∠BOC的平分线,
∵OD是∠BOC的平分线,
∴∠COD=∠BOD=20°,
∴∠AOD=∠BOD+∠AOB=20°+90°=110°,
又∵OE是∠AOD的平分线,
∴∠DOE=$\frac{1}{2}$∠AOD=55°,
∴∠BOE=∠DOE-∠BOD=55°-20°=35°;
(2)同(1)可得∠COD=∠BOD=$\frac{1}{2}α$,
∠AOD=$\frac{1}{2}$α+90°,
∠DOE=$\frac{1}{2}$∠AOD=$\frac{1}{2}$($\frac{1}{2}α$+90°)=$\frac{1}{4}$α+45°,
则∠BOE=$\frac{1}{4}$α+45°-$\frac{1}{2}$α=45°-$\frac{1}{4}$α.
点评 本题考查了角度的计算,理解角平分线的定义是关键.

练习册系列答案
相关题目
9.在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以点C为圆心2cm长为半径的圆与AB的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
10.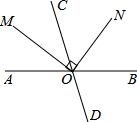 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=30°,则∠CON的度数为( )
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=30°,则∠CON的度数为( )
 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=30°,则∠CON的度数为( )
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=30°,则∠CON的度数为( )| A. | 30° | B. | 40° | C. | 60° | D. | 50° |
 一个正方体的六个面上写有六个连续的整数.如图,是此正方体的展开图,相对面上两个数之和相等,且6个整数之和为45,则n=6.
一个正方体的六个面上写有六个连续的整数.如图,是此正方体的展开图,相对面上两个数之和相等,且6个整数之和为45,则n=6.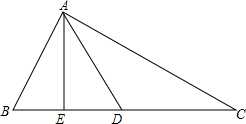 如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线.
如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线. 如图,线段AD和BC相交于点O,AB∥BC,∠D=55°,∠B=45°.求∠AOC的度数.
如图,线段AD和BC相交于点O,AB∥BC,∠D=55°,∠B=45°.求∠AOC的度数.