题目内容
11.若实数m,n满足(m2+n2)(m2+n2-2)-8=0,则m2+n2=4.分析 设x=m2+n2,则原方程变形为x2-2x-8=0,利用因式分解法解方程即可求出x的值,再根据x=m2+n2≥0,即可得出结论.
解答 解:设x=m2+n2,则原方程可化为x•(x-2)-8=0,
整理,得:x2-2x-8=(x+2)(x-4)=0,
解得:x1=-2,x2=4.
∵x=m2+n2≥0,
∴x=4.
故答案为:4.
点评 本题考查了换元法解一元二次方程,熟练掌握换元法解一元二次方程的方法是解题的关键.

练习册系列答案
相关题目
8.一元二次方程x2+2x-2=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
6.在平面直角坐标系中.已知A(0,4).B(-2,0)在坐标轴上确定点P.使△AOP与△AOB相似.则符合条件的点P共有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
16.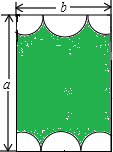 如图,一块长为a,宽为b的长方形草坪,上下开辟的花园,都是由等半径的两个四分之一圆和一个半圆组成,那么中间草坪的面积是( )
如图,一块长为a,宽为b的长方形草坪,上下开辟的花园,都是由等半径的两个四分之一圆和一个半圆组成,那么中间草坪的面积是( )
 如图,一块长为a,宽为b的长方形草坪,上下开辟的花园,都是由等半径的两个四分之一圆和一个半圆组成,那么中间草坪的面积是( )
如图,一块长为a,宽为b的长方形草坪,上下开辟的花园,都是由等半径的两个四分之一圆和一个半圆组成,那么中间草坪的面积是( )| A. | ab-πb2 | B. | ab-$\frac{π}{2}$b2 | C. | ab-$\frac{π}{4}$b2 | D. | ab-$\frac{π}{8}$b2 |
3.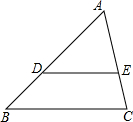 如图,DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比为( )
如图,DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比为( )
 如图,DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比为( )
如图,DE∥BC,AD:DB=2:1,那么△ADE与△ABC的相似比为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | 2 |
1.将一个无盖的正方体纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②),则所剪得直角三角形较短的直角边与较长的直角边的比是 ( )
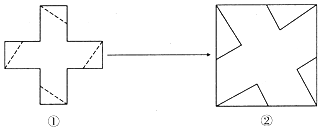

| A. | 1:2 | B. | $\sqrt{3}$:3 | C. | 1:3 | D. | 不能确定 |