题目内容
1.将一个无盖的正方体纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②),则所剪得直角三角形较短的直角边与较长的直角边的比是 ( )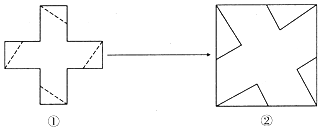
| A. | 1:2 | B. | $\sqrt{3}$:3 | C. | 1:3 | D. | 不能确定 |
分析 直接利用将一个无盖的正方体纸盒展开,得出所剪得的直角三角形较短的边是原正方体棱长的一半,而较长的直角边正好是原正方体的棱长,进而得出答案.
解答 解:由图可得,所剪得的直角三角形较短的边是原正方体棱长的一半,而较长的直角边正好是原正方体的棱长,
所以所剪得的直角三角形较短的与较长的直角边的比是1:2.
故选:A.
点评 本题考查了剪纸的问题,难度不大,以不变应万变,透过现象把握本质,将问题转化为熟悉的知识去解决,同时考查了学生的动手和想象能力.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
16.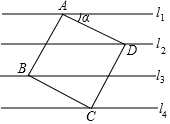 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )
如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )
 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )
如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{3}}{2}$ |
10.若2y-3x=0,则x:y的值等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $-\frac{3}{2}$ | D. | $-\frac{2}{3}$ |
 输入-2,按照如图所示的程序进行运算(完成一个方框内的运算后,把结果输入下一个方框继续进行运算),并写出输出的结果.
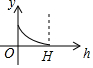
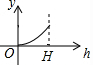
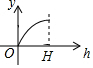
输入-2,按照如图所示的程序进行运算(完成一个方框内的运算后,把结果输入下一个方框继续进行运算),并写出输出的结果.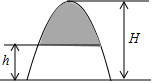 如图所示的图形,是由开口向下的抛物线两边平齐的一部分和一水平线段围成的,设其总高度为H,空白部分的高度是h(0≤h≤H),阴影部分的面积是S,则S随h变化的大致趋势是( )
如图所示的图形,是由开口向下的抛物线两边平齐的一部分和一水平线段围成的,设其总高度为H,空白部分的高度是h(0≤h≤H),阴影部分的面积是S,则S随h变化的大致趋势是( )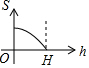
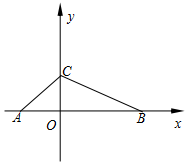 如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-2,0)、B(4,0)、C(0,2).
如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-2,0)、B(4,0)、C(0,2).