题目内容
12．已知∠1=30°，∠1与∠2互为余角，则∠2的度数为60°．分析 根据互余两角之和等于90°，求解即可．
解答 解：∵∠1=30°，∠1与∠2互为余角，
∴∠2=90°-∠1=90°-30°=60°．
故答案为：60°．
点评 本题考查了余角和补角的知识，解答本题的关键在于熟练掌握互余两角之和等于为90°．
练习册系列答案
相关题目
2．四边形ABCD中，∠A=∠B=∠C=90°，下列条件能使这个四边形是正方形的是（ ）
| A． | ∠D=90° | B． | AB=CD | C． | BC=CD | D． | AC=BD |
3．
如图，在矩形ABCD中，∠BOC=120°，AB=5，则BD的长为（ ）
如图，在矩形ABCD中，∠BOC=120°，AB=5，则BD的长为（ ）| A． | 5 | B． | 10 | C． | 12 | D． | 13 |
如图，AC=BC，D是AB的中点，CE∥AB，CE=$\frac{1}{2}$AB．
7．
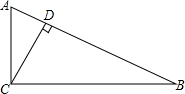如图，在△ABC中，∠ACB=90°，CD为高，AC=4，则下列计算结果错误的是（ ）
如图，在△ABC中，∠ACB=90°，CD为高，AC=4，则下列计算结果错误的是（ ）| A． | 若BC=3，则CD=2.4 | B． | 若∠A=30°，则BD=$\frac{\sqrt{3}}{3}$ | ||
| C． | 若∠A=45°，则AD=2$\sqrt{2}$ | D． | 若BC=2，则S△ADC=$\frac{16}{5}$ |
已知：如图，在矩形ABCD中，点E是BC边上一点，且AE=DE．
如图，在菱形ABCD中，∠B=60°，AB=1，延长AD到点E，使DE=AD，延长CD到点F，使DF=CD，连接AC、CE、EF、AF．
如图，公园内有一小湖，为了测量湖边B、C两点间的距离，小明设计如下方案，选取一个合适的A点，分别找到AB、AC的中点D、E，若测得DE的长为35米，则B、C两点间的距离为70米．