题目内容
5.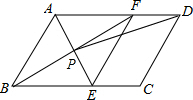 如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求PD.
分析 (1)由四边形ABCD是平行四边形,得到AD∥BC,从而得到∠AFB=∠FBE,再由∠ABF=∠FBE,推出∠ABF=∠AFB,于是得到AB=AF,同理得出AB=BE,于是得出结论;
(2)由菱形的性质得出AE⊥BF,得到∠ABF=30°,∠BAP=∠FAP=60°从而得出AP=2,过点P作PM⊥AD于M,得到PM=$\sqrt{3}$,AM=1,从而得到,DM=5,于是推出结论.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFB=∠FBE,
∵∠ABF=∠FBE,
∴∠ABF=∠AFB,
∴AB=AF,
同理AB=BE,
∴四边形ABEF是菱形;
(2)∵四边形ABEF是菱形,
∴AE⊥BF,
∵∠ABC=60°,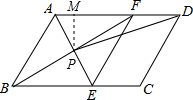
∴∠ABF=30°,∠BAP=∠FAP=60°,
∵AB=4,
∴AP=2,
如图,过点P作PM⊥AD于M,
∴PM=$\sqrt{3}$,AM=1,
∵AD=6,
∴DM=5,
∴PD=$\sqrt{{PM}^{2}{+DM}^{2}}$=$\sqrt{{(\sqrt{3})}^{2}{+5}^{2}}$=2$\sqrt{7}$.
点评 本题主要考查了平行四边形的性质,平行线的性质和菱形的判定,特殊三角形的性质,通过等量代换推出角相等推出等腰三角形是解决问题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
17.要使分式$\frac{1}{x+2}$有意义,则x的取值应满足( )
| A. | x=-2 | B. | x≠2 | C. | x>-2 | D. | x≠-2 |
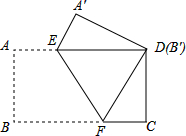 把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.
把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.
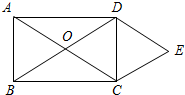 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.