题目内容
10.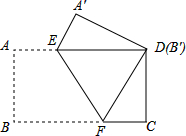 把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.
把一张矩形纸片ABCD按如图方式折叠,使顶点B和D重合,折痕为EF.(1)连接BE,求证:四边形BFDE是菱形;
(2)若AB=8cm,BC=16cm,求线段DF和EF的长.
分析 (1)证得DE=DF,得四边形BFDE是平行四边形,根据折叠的性质知:BF=DF,得四边形BFDE是菱形;
(2)在Rt△DCF中,利用勾股定理可求得DF的长;连接BD,得BD=8$\sqrt{5}$cm,利用S菱形BFDE=$\frac{1}{2}$EF•BD,易得EF的长.
解答 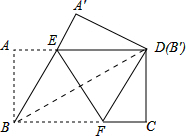 解:(1)由折叠的性质可得∠BFE=∠DFE,
解:(1)由折叠的性质可得∠BFE=∠DFE,
∵AD∥BC,
∴∠BFE=∠DEF,
∴∠DFE=∠DEF,
∴DE=DF,
∴四边形BFDE是平行四边形,
由折叠知,BF=DF.
∴四边形BFDE是菱形;
(3)在Rt△DCF中,设DF=x,则BF=x,CF=16-x,
由勾股定理得:x2=(16-x)2+82,
解得x=10,
DF=10cm,
连接BD.
在Rt△BCD中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=8$\sqrt{5}$,
∵S菱形BFDE=$\frac{1}{2}$EF•BD=BF•DC,
∴$\frac{1}{2}$EF×8$\sqrt{5}$=10×8
解得EF=4$\sqrt{5}$cm.
点评 本题主要考查了勾股定理、平行四边形的判定、菱形的判定和性质,解题的关键是作好辅助线找到相关的三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.-$\frac{1}{5}$的相反数是( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | -$\frac{1}{5}$ | D. | -5 |
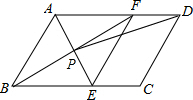 如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.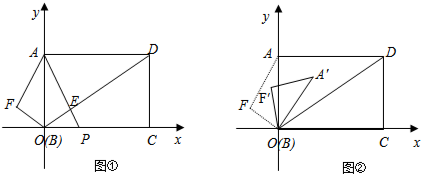
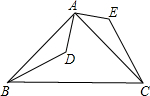 如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是△ABC内一点,连结AD,将线段AD绕点A逆时针旋转90°,得到线段AE,连结BD、CE.求证:BD=CE.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是△ABC内一点,连结AD,将线段AD绕点A逆时针旋转90°,得到线段AE,连结BD、CE.求证:BD=CE.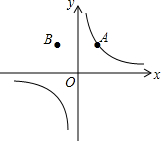 如图,已知点A和B(-1,2)关于y轴对称,反比例函数$y=\frac{k}{x}$的图象经过点A,则k的值为2.
如图,已知点A和B(-1,2)关于y轴对称,反比例函数$y=\frac{k}{x}$的图象经过点A,则k的值为2.