题目内容
15.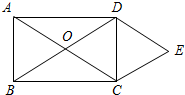 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.(1)求证:四边形OCED是菱形;
(2)若tan∠BAC=$\frac{3}{2}$,菱形OCED的面积为12,求BC的长.
分析 (1)首先由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD=4,即可判定四边形CODE是菱形;
(2)利用矩形和菱形的性质易得OM=$\frac{1}{2}OE$,CM=$\frac{1}{2}$CD,OM=$\frac{1}{2}$BC,再利用菱形的面积公式得OM,求得OC.
解答 (1)证明:∵四边形ABCD是矩形,
∴BD=AC,DO=BO,AO=CO,
∴OD=OC,
∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∴四边形CODE是菱形;
(2)解: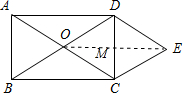 连接OE,
连接OE,
∵四边形CODE是菱形,
∴OE⊥CD,OM=$\frac{1}{2}OE$,CM=$\frac{1}{2}$CD,
∵四边形ABCD是矩形,
∴OM=$\frac{1}{2}$BC,
∵tan∠BAC=$\frac{3}{2}$,
∴tan∠OCM=$\frac{OM}{CM}$=$\frac{3}{2}$,
设OM=3x,则CM=2x,
∵菱形OCED的面积为12,
∴6x•4x=12,
∴x=±$\frac{\sqrt{2}}{2}$(负值舍去),
∴OM=$\frac{3\sqrt{2}}{2}$,
∴BC=3$\sqrt{2}$.
点评 本题主要考查了矩形的性质和菱形的性质和判定,利用菱形的面积等于两对角线的乘积是解答此题的关键.

练习册系列答案
相关题目
3.sin45°的值等于( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
10.八年2班组织了一次经典诵读比赛,甲、乙两组各10人的比赛成绩如下表(10 分制):
(I)甲组数据的中位数是9.5,乙组数据的众数是10;
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是1.4分2,则成绩较为整齐的是乙组.
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是1.4分2,则成绩较为整齐的是乙组.
7.(-2)×3的结果是( )
| A. | 1 | B. | -1 | C. | -5 | D. | -6 |
5.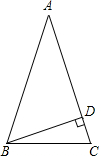 如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )
如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )
 如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )
如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )| A. | 36° | B. | 30° | C. | 24° | D. | 18° |
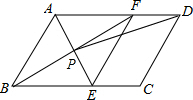 如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.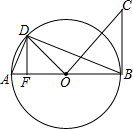 如图,AB是⊙O的直径,BC与⊙O相切于点B,点D在⊙O上,且OD⊥OC,
如图,AB是⊙O的直径,BC与⊙O相切于点B,点D在⊙O上,且OD⊥OC,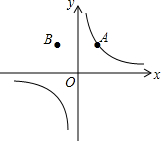 如图,已知点A和B(-1,2)关于y轴对称,反比例函数$y=\frac{k}{x}$的图象经过点A,则k的值为2.
如图,已知点A和B(-1,2)关于y轴对称,反比例函数$y=\frac{k}{x}$的图象经过点A,则k的值为2.