题目内容
8．
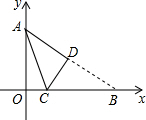已知OA=6，OB=8，将△AOB沿着某直线CD折叠后如图所示，CD与x轴交于点C，与AB交于点D，则点C坐标是（$\frac{7}{4}$，0）．
分析 设C（a，0），根据题意，AC=BC=8-a，然后根据勾股定理列出关于a的方程，解方程即可求得．
解答 解：设C（a，0），
∴OC=a，
∵OA=6，OB=8，
∴AC=BC=8-a，
在RT△AOC中，AC2=OA2+OC2，
∴（8-a）2=a2+62，
解得a=$\frac{7}{4}$，
∴C（$\frac{7}{4}$，0），
故答案为（$\frac{7}{4}$，0）．
点评 本题考查了一次函数的图象与几何变换，翻折的性质以及勾股定理的应用，根据勾股定理列出方程是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
19．原型：如图①，在Rt△ABC中，∠ACB=90°，C是在直线l上的一点，AD⊥l，BE⊥l，垂足分别为D、E．易证△ACD∽△CBE．（不需证明）
应用：点A、B在抛物线y=x2上，且OA⊥OB，连结AB与y轴交于点C，点C的坐标为（0，d）．过点A、B分别作x轴的垂线，垂足为M、N，点M、N的坐标分别为（m，0）、（n，0）．
（1）当OA=OB时，如图②，m=1，d=1；
当OA≠OB，如图③，m=$\frac{2}{3}$时，d=1．
（2）若将抛物线“y=x2”换成“y=2x2”，其他条件不变，当OA=OB时，d=$\frac{1}{2}$；当OA≠OB，m=1时，d=$\frac{1}{2}$．
探究：若将抛物线“y=x2”换成“y=ax2（a＞0）”，其他条件不变，解答下列问题：
（1）完成下列表格．
（2）猜测d与a的关系，并证明其结论．
拓展：如图④，点A、B在抛物线y=ax2（a＞0）上，且OA⊥OB，连结AB与y轴关于点C，AB的延长线与x轴交于点D．AE⊥x轴，垂足为E，当AE=$\frac{4}{3a}$时，△AOE与△CDO的面积之比为4：9．
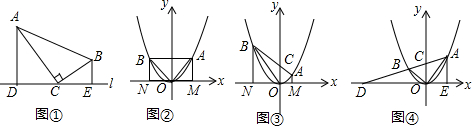
应用：点A、B在抛物线y=x2上，且OA⊥OB，连结AB与y轴交于点C，点C的坐标为（0，d）．过点A、B分别作x轴的垂线，垂足为M、N，点M、N的坐标分别为（m，0）、（n，0）．
（1）当OA=OB时，如图②，m=1，d=1；
当OA≠OB，如图③，m=$\frac{2}{3}$时，d=1．
（2）若将抛物线“y=x2”换成“y=2x2”，其他条件不变，当OA=OB时，d=$\frac{1}{2}$；当OA≠OB，m=1时，d=$\frac{1}{2}$．
探究：若将抛物线“y=x2”换成“y=ax2（a＞0）”，其他条件不变，解答下列问题：
（1）完成下列表格．
| a | 1 | 2 | 3 | $\frac{1}{2}$ |
| d | 1 | $\frac{1}{2}$ | $\frac{1}{3}$ | 2 |
拓展：如图④，点A、B在抛物线y=ax2（a＞0）上，且OA⊥OB，连结AB与y轴关于点C，AB的延长线与x轴交于点D．AE⊥x轴，垂足为E，当AE=$\frac{4}{3a}$时，△AOE与△CDO的面积之比为4：9．
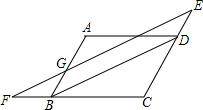如图，在?ABCD中，直线EF∥BD，与CD、CB的延长线分别交于点E、F，交AB、AD于G、H．
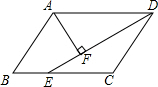如图，?ABCD中，DE平分∠ADC交BC于E，AF⊥DE于F，已知∠DAF=58°，则∠B=64°．
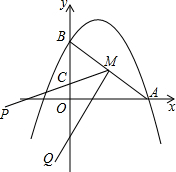如图，抛物线y=-$\frac{1}{2}$x2+x+4与x轴和y轴的正半轴分别交于点A和B．
如图，MN与BC在同一条直线上，且MN=BC=2，点B和点N重合，以MN为底作高为2的等腰△PMN，以BC为边作正方形ABCD，若设△PMN沿射线BC方向平移的距离为x，两图形重合部分的面积为y，则y关于x的函数大致图象是（ ）
18．如果（x+a）（x+b）的结果中不含x的一次项，那么a、b应满足（ ）
| A． | a=b | B． | a=0 | C． | ab=1 | D． | a+b=0 |