Question

12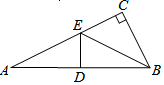．如图，在△ABC中，∠C=90°，D是AB的中点，E是AC边上一点，且 DE⊥AB，连结EB，若AC=6，BC=3，则CE的长为（　　）

• A． $\frac{9}{4}$
• B． $\frac{3}{2}$
• C． $\frac{11}{2}$
• D． $\sqrt{3}$

Answer 1

分析 由线段垂直平分线的性质得出AE=BE，设CE为x，则AE=BE=6-x，由勾股定理得出方程，解方程即可．

解答 解：∵D是AB的中点，DE⊥AB，
∴AE=BE，设CE为x，则AE=BE=6-x，
∵∠C=90°，
∴BC²+CE²=BE²，
即3²+x²=（6-x）²，
解得：x=$\frac{9}{4}$，
∴CE=$\frac{9}{4}$；
故选：A．

点评 本题考查了勾股定理、线段垂直平分线的性质；熟练掌握线段垂直平分线的性质，由勾股定理得出方程是解决问题的关键．