题目内容
2．某商店2016年10月份的利润是2500元，12月份的利润达到3600元．求该商店平均每月利润增长的百分率．分析 设该商店平均每月利润增长的百分率是x，那么11月份的利润为2500（1+x），12月份的利润为2500（1+x）（1+x），然后根据12月份的利润达到3600元即可列出方程，解方程即可．
解答 解：设该商店平均每月利润增长的百分率是x，
依题意得2500（1+x）2=3600，
∴1+x=±1.2，
∴x=0.2=20%或x=-2.2（负值舍去）．
答：该商店平均每月利润增长的百分率是20%．
点评 此题主要考查了一元二次方程的知识，属于增长率的问题，一般公式为原来的量×（1±x）2=后来的量，其中增长用+，减少用-，难度一般．
练习册系列答案
相关题目
12．
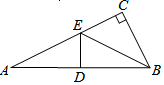如图，在△ABC中，∠C=90°，D是AB的中点，E是AC边上一点，且 DE⊥AB，连结EB，若AC=6，BC=3，则CE的长为（ ）
如图，在△ABC中，∠C=90°，D是AB的中点，E是AC边上一点，且 DE⊥AB，连结EB，若AC=6，BC=3，则CE的长为（ ）| A． | $\frac{9}{4}$ | B． | $\frac{3}{2}$ | C． | $\frac{11}{2}$ | D． | $\sqrt{3}$ |
13．如图，在两个形状、大小完全相同的大长方形内，分别互不重叠地放入四个如图③的小长方形后得图①、图②，已知大长方形的长为a，两个大长方形未被覆盖部分分别用阴影表示，则图①阴影部分周长与图②阴影部分周长的差是（ ）（用a的代数式表示）（ ）
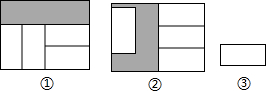
| A． | -a | B． | -$\frac{1}{2}$a | C． | $\frac{1}{2}$a | D． | a |
10．若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根，则k的取值范围是（ ）
| A． | k＞1 | B． | k＞-1且k≠0 | C． | k≥-1且k≠0 | D． | k＜1且k≠0 |
如图，AB是⊙O的直径，C、D是⊙O上的两点，若∠ABD=62°，则∠BCD=28°．
如图，在平面直角坐标系中，点A、B、C的坐标分别为（-1，3）、（-4，1）、（-2，1），先将△ABC沿一确定方向平移得到△A1B1C1，点B的对应点B1的坐标是（1，2），再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2，点A1的对应点为点A2．
12．一元二次方程x2+2x+4=0的根的情况是（ ）
| A． | 有两个相等的实数根 | B． | 有两个不相等的实数根 | ||
| C． | 只有一个实数根 | D． | 没有实数根 |