题目内容
7.有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则关于x的不等式组$\left\{\begin{array}{l}{4x≥3(x+1)}\\{2x-\frac{x-1}{2}<a}\end{array}\right.$有解的概率为$\frac{4}{9}$.分析 由关于x的不等式组$\left\{\begin{array}{l}{4x≥3(x+1)}\\{2x-\frac{x-1}{2}<a}\end{array}\right.$有解,可求得a>5,然后利用概率公式求解即可求得答案.
解答 解:$\left\{\begin{array}{l}{4x≥3(x+1)①}\\{2x-\frac{x-1}{2}<a②}\end{array}\right.$,
由①得:x≥3,
由②得:x<$\frac{2a-1}{3}$,
∵关于x的不等式组$\left\{\begin{array}{l}{4x≥3(x+1)}\\{2x-\frac{x-1}{2}<a}\end{array}\right.$有解,
∴$\frac{2a-1}{3}$>3,
解得:a>5,
∴使关于x的不等式组$\left\{\begin{array}{l}{4x≥3(x+1)}\\{2x-\frac{x-1}{2}<a}\end{array}\right.$有解的概率为:$\frac{4}{9}$.
故答案为:$\frac{4}{9}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
18.下列判断正确的是( )
| A. | -$\frac{3}{5}$<-$\frac{4}{7}$ | B. | x-1是有理数,它的倒数是$\frac{1}{x-1}$ | ||
| C. | 若|a|=|b|,则a=b | D. | 若|a|=-a,则a<0 |
15. 如图所示的几何体,从左面看到的形状图是( )
如图所示的几何体,从左面看到的形状图是( )
 如图所示的几何体,从左面看到的形状图是( )
如图所示的几何体,从左面看到的形状图是( )| A. |  | B. |  | C. |  | D. |  |
12.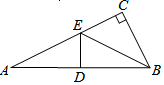 如图,在△ABC中,∠C=90°,D是AB的中点,E是AC边上一点,且 DE⊥AB,连结EB,若AC=6,BC=3,则CE的长为( )
如图,在△ABC中,∠C=90°,D是AB的中点,E是AC边上一点,且 DE⊥AB,连结EB,若AC=6,BC=3,则CE的长为( )
 如图,在△ABC中,∠C=90°,D是AB的中点,E是AC边上一点,且 DE⊥AB,连结EB,若AC=6,BC=3,则CE的长为( )
如图,在△ABC中,∠C=90°,D是AB的中点,E是AC边上一点,且 DE⊥AB,连结EB,若AC=6,BC=3,则CE的长为( )| A. | $\frac{9}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{11}{2}$ | D. | $\sqrt{3}$ |
16.下列英文字母既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
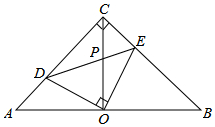 如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①∠AOD=∠COE;②图形中全等的三角形有3对; ③△ABC的面积等于四边形CDOE的面积的2倍;④CD+CE=$\sqrt{2}$OA;⑤AD2+BE2=2OD2,其中正确的结论有( )
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①∠AOD=∠COE;②图形中全等的三角形有3对; ③△ABC的面积等于四边形CDOE的面积的2倍;④CD+CE=$\sqrt{2}$OA;⑤AD2+BE2=2OD2,其中正确的结论有( )
 如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABD=62°,则∠BCD=28°.
如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠ABD=62°,则∠BCD=28°.