题目内容
17.已知∠AOB=90°,OM是∠AOB的平分线,按以下要求解答问题: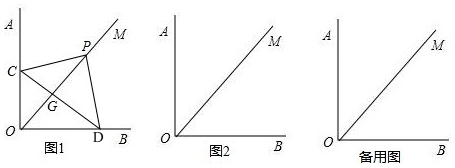
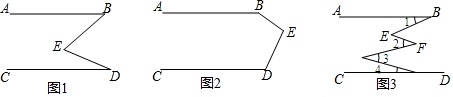
(1)将一块含45°角的直角三角板的直角顶点P在射线OM上移动,两直角边分别与OA、OB交于点C,D,在图1中,点G是CD与OP的交点,且PG=$\frac{\sqrt{3}}{2}$PD,求:△POD与△PDG的面积之比;
(2)将三角板的直角顶点P在射线OM上移动,一直角边与OB交于点D,OD=1,另一直角边与直线OA、OB分别交于点C、E,使以P,D,E为顶点的三角形与△OCD相似,在图2中作出图形,并求OP的长.
分析 (1)先判定△POD∽△PDG,然后根据相似三角形的性质和已知条件就可以求出△POD与△PDG的面积比;
(2)分两种情况进行讨论:①当C在OA上时;②当C在OA延长线上时,分别根据相似三角形的性质以及全等三角形的性质进行求解.
解答 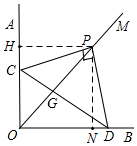 解:(1)如图1,过P作PH⊥OA,PN⊥OB,垂足分别为H,N,则∠HPN=90°,
解:(1)如图1,过P作PH⊥OA,PN⊥OB,垂足分别为H,N,则∠HPN=90°,
∴∠HPC+∠CPN=90°,
∵∠CPN+∠NPD=90°,
∴∠HPC=∠NPD,
∵OM是∠AOB的平分线,
∴PH=PN,
又∵∠PHC=∠PND=90°,
∴△PCH≌△PDN,
∴PC=PD,
∴∠PDG=45°,
∵∠POD=45°,
∴∠PDG=∠POD,
∵∠GPD=∠DPO,
∴△POD∽△PDG,
∴$\frac{{S}_{△POD}}{{S}_{△PDG}}$=($\frac{PD}{PG}$)2=$\frac{4}{3}$;
(2)分两种情况:
①如图,若PC与边OA相交,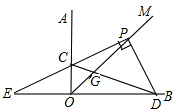
∵∠PDE>∠CDO,
当△PDE∽△OCD时,∠CDO=∠PED,
∴CE=CD,
∵CO⊥ED,
∴OE=OD,
∴OP=$\frac{1}{2}$ED=OD=1;
②如图,若PC与边OA的反向延长线相交,
过P作PH⊥OA,PN⊥OB,垂足分别为H,N,
∵∠PED>∠EDC,
当△PDE∽△ODC时,∠PDE=∠ODC,
∵∠OEC=∠PED,
∴∠PDE=∠HCP,
∵PH=PN,Rt△PHC≌Rt△PND,
∴HC=ND,PC=PD,
∴∠PDC=45°,
∴∠PDO=∠PCH=22.5°,
∴∠OPC=180°-∠POC-∠OCP=22.5°,
∴OP=OC.
设OP=x,则OH=ON=$\frac{\sqrt{2}}{2}$x,
∴HC=DN=OD-ON=1-$\frac{\sqrt{2}}{2}$x,
∵HC=HO+OC=$\frac{\sqrt{2}}{2}$x+x,
∴1-$\frac{\sqrt{2}}{2}$x=$\frac{\sqrt{2}}{2}$x+x,
∴x=$\sqrt{2}$-1,
即OP=$\sqrt{2}$-1.
点评 本题主要考查了直角三角形斜边上中线的性质,角平分线的性质,全等三角形的判定与性质以及相似三角形的判定和性质等知识点的综合应用,根据三角形相似或全等得出线段之间以及角之间的关系是解题的关键.

 字词句段篇系列答案
字词句段篇系列答案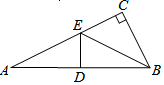 如图,在△ABC中,∠C=90°,D是AB的中点,E是AC边上一点,且 DE⊥AB,连结EB,若AC=6,BC=3,则CE的长为( )
如图,在△ABC中,∠C=90°,D是AB的中点,E是AC边上一点,且 DE⊥AB,连结EB,若AC=6,BC=3,则CE的长为( )| A. | $\frac{9}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{11}{2}$ | D. | $\sqrt{3}$ |
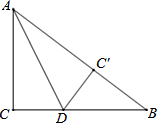 如图,有一块直角三角形ABC纸片,∠ACB=90°,AC=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,点C与点C'重合,求CD的长.
如图,有一块直角三角形ABC纸片,∠ACB=90°,AC=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,点C与点C'重合,求CD的长.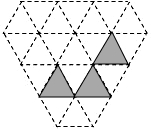 如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你再只涂黑一个小三角形,使它与阴影部分合起来所构成的完整图形是一个轴对称图形.
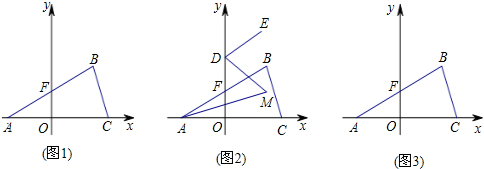
如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你再只涂黑一个小三角形,使它与阴影部分合起来所构成的完整图形是一个轴对称图形.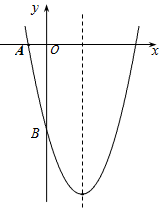 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点