题目内容
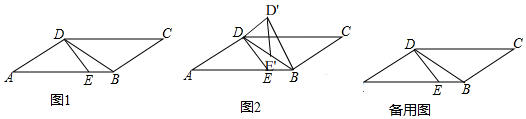
10.如图1,平行四边形ABCD中,AD=BD,∠A=30°,DE=2$\sqrt{2}$,点E在AB边上且∠AED=45°.(1)求∠BDE的度数;
(2)将图1中的△BED绕点B顺时针旋转α(0°<α≤360°)得到△BE′D′.
①当点E′恰好落在BD边上时,如图2所示,连接D′D并延长交AB于点F.求证:AF=BE′;
②在△BED旋转的过程中,当∠BAD′最大时,求线段AD′的长.
分析 (1)先利用等腰三角形的性质求出∠ABD,再用三角形的外角即可得出结论;
(2)①先求出∠BDD=75°,利用三角形的外角得出∠BFD=45°,进而得出∠AFD=∠BED=135°,即可判断出△ADF≌△DBE(ASA),即可;
②先利用等腰直角三角形的性质求出DF,再利用含30°的直角三角形的性质求出AD=BD=4,AB=2AF=4$\sqrt{3}$,
最后用勾股定理即可得出结论.
解答 解:(1)∵AD=BD,∠A=30°,
∴∠ABD=∠A=30°,
∵∠AED=45°,
∴∠BDE=∠AED-∠ABD=45°-30°=15°,
(2)①如图1, 连接D'D并延长交AB于F,
连接D'D并延长交AB于F,
由旋转知,∠DBD'=∠ABD=30°,BD'=BD,
∴∠BDD'=$\frac{1}{2}$(180°-∠DBD')=75°,
∴∠BFD'=∠BDD'-∠ABD=75°-30°=45°(三角形的一个外角等于与它不相邻的两内角的和)
∵∠AED=45°,
∴∠BFD'=∠AED,
∵∠AFD+∠BFD'=180°,∠AED+∠BED=180°,
∴∠AFD=∠BED=135°,
在△ADF和△DBE中,$\left\{\begin{array}{l}{∠AFD=∠BED=135°}\\{∠A=∠EBD}\\{AD=BD}\end{array}\right.$,
∴△ADF≌△DBE(ASA),
∴AF=BE,由旋转知,BE'=BE,
∴AF=BE';
②如图2,
过点D作DG⊥AB于G,
在Rt△DEG中,∠AED=45°,DE=2$\sqrt{2}$,
∴DG=2,
在Rt△ADG中,∠BAD=30°.DG=2,
∴AD=4,AG=2$\sqrt{3}$,
∵AD=BD=4,DG⊥AB,
∴AB=2AG=4$\sqrt{3}$,
∵△BDE绕点B旋转的过程中,点D是以点B为圆心,BD为半径的圆,
∴AD'与⊙B相切时,∠BAD'最大,
∴∠AD'B=90°,
由旋转知,BD'=BD=4,
在Rt△ABD'中,BD'=4.AB=4$\sqrt{3}$,
根据勾股定理得,AD'=$\sqrt{A{B}^{2}-BD{'}^{2}}$=4$\sqrt{2}$.
点评 此题是三角形综合题,主要考查了旋转的性质,全等三角形的判定和性质,等腰三角形的性质,等腰直角三角形的性质,30°的直角三角形的性质,勾股定理,解(1)的关键是求出∠ABD的度数,解(2)的关键是判断出∠AFD=∠BED=135°,解(3)的关键是判断出AD与圆B相切时,∠BAD'最大.

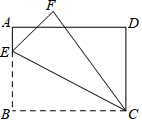 如图,矩形ABCD中,AB=4,BC=6,E为AB上一点,将△BCE沿CE翻折至△FCE,EF与AD相交于点G,且AG=FG,则线段AE的长为1.
如图,矩形ABCD中,AB=4,BC=6,E为AB上一点,将△BCE沿CE翻折至△FCE,EF与AD相交于点G,且AG=FG,则线段AE的长为1.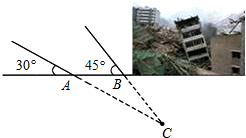 如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到地下C处有生命迹象.已知A,B两点相距8米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度(结果保留根号).
如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A,B两个探测点探测到地下C处有生命迹象.已知A,B两点相距8米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度(结果保留根号).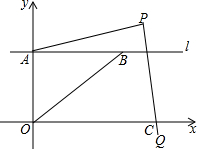 如图,在平面直角坐标系中,直线l∥x轴,交y轴于点A,第一象限内的点B在直线l上,连接OB,动点P满足∠APQ=90°,PQ交x轴于点C,
如图,在平面直角坐标系中,直线l∥x轴,交y轴于点A,第一象限内的点B在直线l上,连接OB,动点P满足∠APQ=90°,PQ交x轴于点C,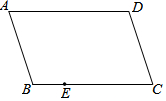 如图,ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.画出满足题意的点F,并简要说明你的画图过程.
如图,ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.画出满足题意的点F,并简要说明你的画图过程.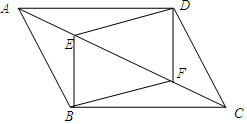 如图,已知E、F是?ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC,连结DE、BF.求证:DE=BF.
如图,已知E、F是?ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC,连结DE、BF.求证:DE=BF.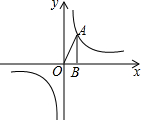 如图,点A为反比例函数y=$\frac{k}{x}$图象上的一点,过点作AB⊥x轴于点B,连接OA,若△OAB的面积为4,则k=8.
如图,点A为反比例函数y=$\frac{k}{x}$图象上的一点,过点作AB⊥x轴于点B,连接OA,若△OAB的面积为4,则k=8.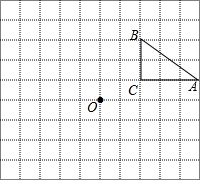 如图,下列网格中,每个小正方形的边长都为1,点A、B、C都在格点上.
如图,下列网格中,每个小正方形的边长都为1,点A、B、C都在格点上.