题目内容
10．
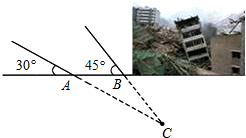如图，某煤矿因不按规定操作发生瓦斯爆炸，救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面A，B两个探测点探测到地下C处有生命迹象．已知A，B两点相距8米，探测线与地面的夹角分别是30°和45°，试确定生命所在点C的深度（结果保留根号）．
分析 根据题意作出合适的辅助线，然后根据特殊角的三角函数值，即可求得生命所在点C的深度．
解答 
解：作CD⊥AB交AB的延长线于点D，如右图所示，
由已知可得，
AB=8米，∠CBD=45°，∠CAD=30°，
∴AD=$\frac{CD}{tan30°}$，BD=$\frac{CD}{tan45°}$，
∴AB=AD-AB=$\frac{CD}{tan30°}-\frac{CD}{tan45°}$，
即8=$\frac{CD}{\frac{\sqrt{3}}{3}}-\frac{CD}{1}$，
解得，CD=$（4\sqrt{3}+4）$米，
即生命所在点C的深度是$（4\sqrt{3}+4）$米．
点评 本题考查解直角三角形的应用，解答本题的关键是明确题意，利用特殊角的三角函数值解答．
练习册系列答案
天天向上口算本系列答案
相关题目
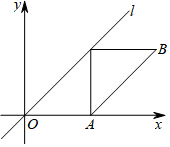如图，在平面直角坐标系中，已知点A（$\frac{3}{2}$$\sqrt{2}$，0），点B在第一象限，且AB与直线l：y=x平行，AB长为4，若点P是直线l上的动点，则△PAB的内切圆面积的最大值为$\frac{1}{4}$π．
18．如图的几何体中，主视图是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
5．若x≠0．m是正整数．则下列各式中正确的是（ ）
| A． | x-m=（$\frac{1}{x}$）m | B． | x-m=-xm | C． | x-2m=$\frac{2}{{x}^{m}}$ | D． | （xm）-3=$\frac{m}{{x}^{3}}$ |
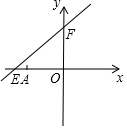如图，直线y=kx+6与x轴分别交于E、F．点E坐标为（-8，0），点A的坐标为（-6，0）．