题目内容

13．解方程：$\frac{3}{{x}^{2}-1}$-$\frac{x}{x+1}$=1．

分析 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．

解答 解：去分母得：3-x2+x=x2-1，即2x2-x-4=0，
解得：x=$\frac{1±\sqrt{33}}{4}$，
经检验x=$\frac{1±\sqrt{33}}{4}$是分式方程的解．

点评 此题考查了解分式方程，利用转化的思想，解分式方程注意要检验．

练习册系列答案
相关题目
3．如图，抛物线y=-$\frac{\sqrt{3}}{9}$x2+$\frac{4\sqrt{3}}{3}$x与x轴交于O、A两点，抛物线的对称轴与x轴交于点B，平行于x轴的直线CD交抛物线于C（9，m）、D两点（C点在D点的右边）．
（1）填空：m=3$\sqrt{3}$，抛物线的对称轴x=6．
（2）在四边形OBCD中，动点P从点D出发沿折线DCB向终点B以2单位/秒的速度运动，同时动点Q从点A出发沿x轴负半轴方向以1单位/秒的速度运动，当点P到达终点时停止运动，设运动时间为t秒，把四边形OBCD沿PQ翻折，翻折后点D的对应点为点E．
①当点E落在直线BD上时，求t的值；
②是否存在t的值，使点E落在x轴上，若存在，求出t的值；若不存在，请说明理由．
（参考数据：362=1296，482=2304）
4．下列运算正确的是（　　）
A．4a•3b=12abB．4a+3b=7abC．（a-b）2=a2-b2D．（-ab1）2=ab3
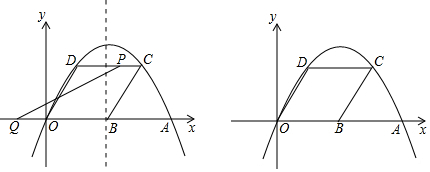
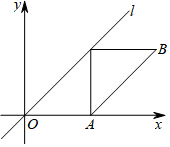1．如图，在平面直角坐标系中，已知点A（$\frac{3}{2}$$\sqrt{2}$，0），点B在第一象限，且AB与直线l：y=x平行，AB长为4，若点P是直线l上的动点，则△PAB的内切圆面积的最大值为$\frac{1}{4}$π．
8．已知，如图，在四边形ABCD中，AD∥BC，点E，F为对角线AC上两点，且AF=CE，DF∥BE．求证：四边形ABCD为平行四边形．
18．如图的几何体中，主视图是中心对称图形的是（　　）
A．B．C．D．
5．若x≠0．m是正整数．则下列各式中正确的是（　　）
A．x-m=（$\frac{1}{x}$）mB．x-m=-xmC．x-2m=$\frac{2}{{x}^{m}}$D．（xm）-3=$\frac{m}{{x}^{3}}$
10．如图1，平行四边形ABCD中，AD=BD，∠A=30°，DE=2$\sqrt{2}$，点E在AB边上且∠AED=45°．
（1）求∠BDE的度数；
（2）将图1中的△BED绕点B顺时针旋转α（0°＜α≤360°）得到△BE′D′．
①当点E′恰好落在BD边上时，如图2所示，连接D′D并延长交AB于点F．求证：AF=BE′；
②在△BED旋转的过程中，当∠BAD′最大时，求线段AD′的长．
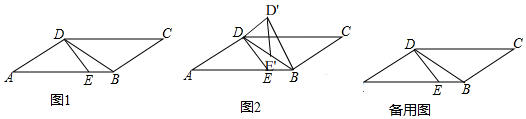
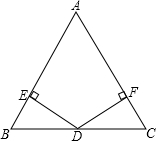11．如图，已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F．
（1）求证：DE=DF；
（2）若∠A=60°，BE=2，求△ABC的周长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网