题目内容
15.已知二次函数y=ax2+$\frac{1}{3}$x-$\frac{5}{3}$的图象交y轴于点C,与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,1).(1)求a和k的值;
(2)求二次函数图象的顶点B的坐标,并判断点B是否在反比例函数的图象上.
分析 (1)将点A(4,1)分别代入二次函数y=ax2+$\frac{1}{3}$x-$\frac{5}{3}$与反比例函数y=$\frac{k}{x}$,求得a和k即可;
(2)根据顶点的公式(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)求点B坐标,再进行判断即可.
解答 解:(1)点A(4,1)分别代入二次函数y=ax2+$\frac{1}{3}$x-$\frac{5}{3}$与反比例函数y=$\frac{k}{x}$,
得16a+$\frac{4}{3}$-$\frac{5}{3}$=1,1=$\frac{k}{4}$,
解得a=$\frac{1}{12}$,k=4;
(2)∵a=$\frac{1}{12}$,b=$\frac{1}{3}$,c=-$\frac{5}{3}$,
∴-$\frac{b}{2a}$=-$\frac{\frac{1}{3}}{\frac{1}{12}}$×$\frac{1}{2}$=-2,
$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×\frac{1}{12}×(-\frac{5}{3})-(\frac{1}{3})^{2}}{4×\frac{1}{12}}$=-2,
∴顶点B的坐标(-2,-2),
把x=-2代入y=$\frac{4}{x}$,得y=-2,
∴点B 在反比例函数图象上.
点评 本题考查了二次函数的性质以及反比例函数图象上点的特征,涉及知识点:用待定系数法求二次函数的解析式、反比例函数的解析式,是一道综合题目,难度不大.

练习册系列答案
相关题目
3.某班有50名同学,期末考试优秀的学生人数及科目如表:
这里,一科优秀者包括两、三科优秀者,两科优秀者里也包括三科优秀者,试说明上述统计表的错误.
| 单科 | 两科 | 三科 | |||||
| 科目 | 数学 | 英语 | 语文 | 语文 数学 | 英语 数学 | 英语 语文 | 语文、数学、英语 |
| 人数 | 32 | 31 | 29 | 16 | 17 | 18 | 10 |
7.下列计算正确的是( )
| A. | 2t-t=2 | B. | t2•t3=t6 | C. | (-t2)3=-t5 | D. | t3÷t2=t |
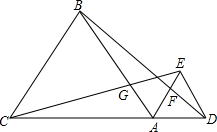 如图,A是CD上的一点,△ABC,△ADE都是正三角形,求证:(1)CE=BD;(2)CG=BF.
如图,A是CD上的一点,△ABC,△ADE都是正三角形,求证:(1)CE=BD;(2)CG=BF.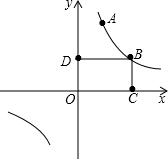 如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.
如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.