Question

6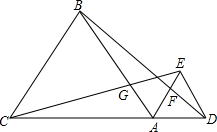．如图，A是CD上的一点，△ABC，△ADE都是正三角形，求证：（1）CE=BD；（2）CG=BF．

Answer 1

分析 （1）如图，首先运用等边三角形的性质证明AC=AB、AD=AE、∠CAE=∠BAD，进而证明△CAE≌△BAD，即可解决问题．
（2）如图，首先证明∠CAG=∠BAF=60°，进而运用ASA公理证明△CAG≌△BAF，即可解决问题．

解答 证明：（1）如图，∵△ABC，△ADE都是正三角形，
∴AC=AB，AD=AE；∠BAC=∠DAE=60°，
∴∠CAE=∠BAD；
在△CAE与△BAD中，
$\left\{\begin{array}{l}{CA=BA}\\{∠CAE=∠BAD}\\{AE=AD}\end{array}\right.$，
∴△CAE≌△BAD（SAS），
∴CE=BD．
（2）∵∠CAB=∠DAE=60°，
∴∠BAE=60°，∠CAG=∠BAF=60°；
∵△CAE≌△BAD，
∴∠ACG=∠ABF；
在△CAG与△BAF中，
$\left\{\begin{array}{l}{∠ACG=∠ABF}\\{AC=AB}\\{∠CAG=∠BAF}\end{array}\right.$，
∴△CAG≌△BAF（ASA），
∴CG=BF．

点评 该题主要考查了等边三角形的性质、全等三角形的判定等几何知识点及其应用问题；牢固掌握等边三角形的性质、全等三角形的判定等几何知识点是基础，灵活运用、解题是关键．