题目内容
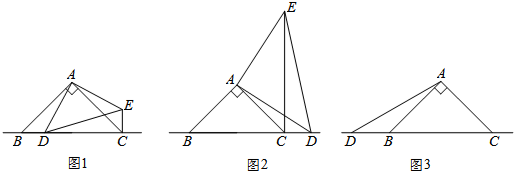
5.已知Rt△ABC,AB=AC,∠BAC=90°,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作Rt△ADE(其中AD=AE,∠DAE=90°A、D、E按逆时针排列),连接CE.(1)如图1,当点D在边BC上时,
①请写出BD和CE之间存在数量关系和位置关系,并说明理由;
②$\sqrt{2}$AC=CE+CD的关系是否成立,并说明理由;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,(1)中AC、CE、CD之间存在的数量关系是否成立?若不成立,请直接写出AC、CE、CD之间存在的数量关系,不证明.
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形(要求:尺规作图,不写作法,保留作图痕迹),并直接写出AC、CE、CD之间存在的数量关系,不证明.
分析 (1)①根据AB=AC,∠BAC=90°,AD=AE,∠DAE=90°,证△BAD≌△CAF,推出CE=BD,CE⊥BD即可;
②由△ABC是等腰直角三角形,得到∠ABC=∠ACB=45°,即可得出结论;
(2)求出∠BAD=∠CAE,根据SAS证△BAD≌△CAE,推出BD=CE即可;
(3)画出图形后,根据SAS证△BAD≌△CAE,推出CE=BD即可.
解答 (1)证明:①∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵AD=AE,∠DAE=90°,
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE,
在△ABD与△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AF}\end{array}\right.$,
∴△ABD≌△ACE,
∴BD=CE,∠ABC=∠ACE=45°,
∴∠ECB=90°,
∴BD⊥CE;
②由①得BD=CE,
∴BC=$\sqrt{2}$AC,
∵BC=BD+CD=CE+CD,
∴$\sqrt{2}$AC=CE+CD;
(2)解:存在数量关系为:CE=$\sqrt{2}$AC+CD;
理由:由(1)同理可得
在△ABD与△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AF}\end{array}\right.$,
∴△ABD≌△ACE,
∴BD=CE,
∴BD=CE,
在等腰直角三角形ABC中,
BC=$\sqrt{2}$AC,
∴BD=BC+CD=$\sqrt{2}$C+CD,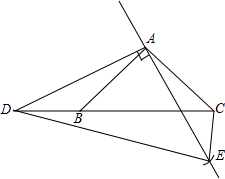
∴CE=$\sqrt{2}$AC+CD;
(3)如图所示:CD=$\sqrt{2}$AC+CE;
理由:由(1)同理
在△ABD与△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AF}\end{array}\right.$,
∴△ABD≌△ACE,
∴BD=CE,
∴BD=CE,
在等腰直角三角形ABC中,
BC=$\sqrt{2}$AC,
∴CD=BC+BD=$\sqrt{2}$AC+CE.
点评 本题考查了全等三角形的性质和判定,等腰直角三角形的性质,正方形的性质的应用,主要考查学生的推理能力,注意:证明过程类似,题目具有一定的代表性,难度适中.

 名校课堂系列答案
名校课堂系列答案 已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:
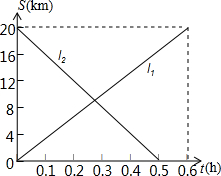 甲、乙两辆摩托车分别从A、B两地同时出发相向而行,两辆摩托车与A地的距离S(km)与行驶时间t(min)之间的函数关系如图,则下列说法中正确的有( )
甲、乙两辆摩托车分别从A、B两地同时出发相向而行,两辆摩托车与A地的距离S(km)与行驶时间t(min)之间的函数关系如图,则下列说法中正确的有( ) 如图,A、P、B、C是⊙O上的四点,∠APC=∠BPC=60°,AB与PC交于点Q;
如图,A、P、B、C是⊙O上的四点,∠APC=∠BPC=60°,AB与PC交于点Q;