题目内容
5.(1)计算:(-$\frac{1}{3}$)-1-$\sqrt{18}$+($\sqrt{3}$-$\sqrt{2}$)0+6sin45°(2)化简:1-$\frac{x-2}{x+1}$÷$\frac{{x}^{2}-4}{{x}^{2}+2x+1}$.
分析 (1)原式第一项利用负指数幂法则计算,第二项化为最简二次根式,第三项利用零指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果;
(2)原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=-3-3$\sqrt{2}$+1+6×$\frac{\sqrt{2}}{2}$=-2;
(2)原式=1-$\frac{x-2}{x+1}$•$\frac{(x+1)^{2}}{(x+2)(x-2)}$=1-$\frac{x+1}{x+2}$=$\frac{1}{x+2}$.
点评 此题考查了实数的运算,以及分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.-3的倒数为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
20.若分式$\frac{1}{x+1}$有意义,则x的取值范围是( )
| A. | x≠1 | B. | x≠-1 | C. | x≥-1 | D. | x>-1 |
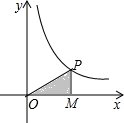 如图,点P为反比例函数y=$\frac{16}{x}$在第一象限图象上的动点,过点P作x轴的垂线,垂足为M,则三角形OPM的面积为8.
如图,点P为反比例函数y=$\frac{16}{x}$在第一象限图象上的动点,过点P作x轴的垂线,垂足为M,则三角形OPM的面积为8.