题目内容
4.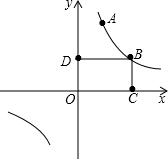 如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.
如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.(1)求反比例函数的解析式;
(2)求OB的长.
分析 (1)把A(2,6)代入y=$\frac{k}{x}$即可得到结果.
(2)连接OB,由点B在反比例函数图象上,得到OC•BC=12,由四边形OCBD的周长为14,得到OC+BC=7,解得OC,BC,结论可求.
解答 解:(1)把A(2,6)代入y=$\frac{k}{x}$得,
∴k=12,
∴反比例函数的解析式为:y=$\frac{12}{x}$;
(2)连接OB,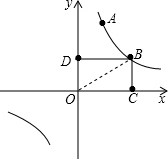
∵点B在反比例函数图象上,
∴OC•BC=12,
∵四边形OCBD的周长为14,
∴OC+BC=7,
∴OC=3,BC=4,或BC=3,OC=4,
∵BC⊥x轴于C,
∴∠OCB=90°,
∴OB=$\sqrt{{3}^{2}{+4}^{2}}$=5.
点评 本题考查了反比例函数图象上点的坐标特征经过函数的某点一定在函数的图象上,待定系数法求反比例函数的解析式,勾股定理,用待定系数法求函数的解析式是常见的题型.

练习册系列答案
相关题目
9.某校园足球队由13位男生组成,体育课上统计了所有男生所穿运动鞋的尺码,列表为:
则这13双运动鞋尺码的众数和中位数分别是( )
| 尺码(单位:码) | 38 | 39 | 40 | 41 | 42 |
| 数量(单位:双) | 2 | 5 | 3 | 1 | 2 |
| A. | 40码、39码 | B. | 39码、40码 | C. | 39码、39码 | D. | 40码、40码 |
16.-3的倒数为( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
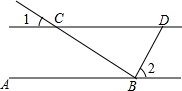 如图所示,AB∥CD,CB⊥DB,∠1=30°,则∠2=60°.
如图所示,AB∥CD,CB⊥DB,∠1=30°,则∠2=60°.