题目内容
2．
如图，抛物线y=ax2+bx+c与y轴正半轴相交，其顶点坐标为（-$\frac{1}{2}$，1），有下列结论：①ac＜0；②a-b=1；③4ac＜b2；④a-b+c＜0，其中正确结论的个数是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 ①根据抛物线的开口方向和抛物线与y轴的交点坐标即可确定；
②根据抛物线的对称轴即可判定；
③根据抛物线与x轴的交点情况即可判定；
④由a-b=0，c＞0，即可判定a-b+c＞0．
解答 解：①∵抛物线开口向下，∴a＜0，∵抛物线与y轴正半轴相交，∴c＞0，∴ac＜0，故①正确；
②∵抛物线的对称轴为x=-$\frac{1}{2}$，∴x=-$\frac{b}{2a}$=-$\frac{1}{2}$，∴a-b=0，故②错误；
③∵抛物线与x轴有两个交点，∴b2-4ac＞0，∴4ac＜b2，故③正确；
④∵a-b=0，c＞0，∴a-b+c＞0，故④错误．
其中正确的是①③．
故选B．
点评 此题主要考查二次函数图象与系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数的自变量与对应的函数值，顶点坐标的熟练运用．
练习册系列答案
阅读快车系列答案
相关题目
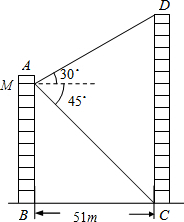如图所示，两个建筑物AB和CD的水平距离为51m，某同学住在建筑物AB内10楼M室，他观测建筑物CD楼的顶部D处的仰角为30°，测得底部C处的俯角为45°，求建筑物CD的高度．（$\sqrt{3}$取1.73，结果保留整数）
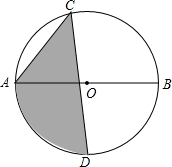如图，⊙O的直径AB为10，弦AC为6，△ACB的平分线交⊙O于点D，则图中阴影部分的面积为$\frac{17}{2}$+$\frac{25π}{4}$．
如图点B，E，C，F在同一条直线上，AB=DE，AC=DF，BE=CF，∠A=43°．
7．
如图，CD为△ABC的中线，且CD⊥AC，O为BC边上一点，以O为圆心，0C为长半径作⊙O，若⊙O与AB恰好相切于点D，则tanB=（ ）
如图，CD为△ABC的中线，且CD⊥AC，O为BC边上一点，以O为圆心，0C为长半径作⊙O，若⊙O与AB恰好相切于点D，则tanB=（ ）| A． | $\frac{1}{3}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{3}{8}$ | D． | $\frac{1}{2}$ |
如图，⊙O为△ABC的外接圆，AB为⊙O的直径，延长AB到点E，连结EC，且∠BCE=∠BAC．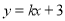
经过点A（-1,2）且与X轴交于点B，点B的坐标是（ ）