题目内容
14. 如图,⊙O为△ABC的外接圆,AB为⊙O的直径,延长AB到点E,连结EC,且∠BCE=∠BAC.
如图,⊙O为△ABC的外接圆,AB为⊙O的直径,延长AB到点E,连结EC,且∠BCE=∠BAC.(1)求证:EC是⊙O的切线.
(2)过点A作AD⊥EC交EC的延长线于点D,若AD=5,DE=12,求⊙O的半径.
分析 (1)连结OC,根据圆周角定理由AB是⊙O的直径得∠1+∠2=90°,而∠1=∠A,∠A=∠BCE,所以∠BCE=∠1,即∠BCE+∠2=90°,然后根据切线的判定定理即可得到EC是⊙O的切线;
(2)设⊙O的半径为r,在Rt△ADE中利用勾股定理计算出AE=13,则OE=13-r,OC=r,证明△EOC∽△EAD,利用相似比得到$\frac{OC}{AD}$=$\frac{EO}{EA}$,即$\frac{r}{5}$=$\frac{13-r}{13}$,然后解方程即可得到圆的半径.
解答 (1)证明:连结OC,如图,
∵AB是⊙O的直径
∴∠ACB=90°,即∠BCO+∠ACO=90°,
∵OC=OA,
∴∠OCA=∠BAC,
又∵∠BCE=∠BAC,
∴∠BCE=∠OCA,
∴∠BCE+∠BCO=90°,
∴OC⊥EC,
∴EC是⊙O的切线;
(2)解:设⊙O的半径为r,
在Rt△ADE中,AD=5,ED=12,AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=13,
∴OE=13-r,OC=r
∵OC⊥EC,
∵AD⊥EC,
∴OC∥AD,
∴△EOC∽△EAD,
∴$\frac{OC}{AD}$=$\frac{EO}{EA}$,即$\frac{r}{5}$=$\frac{13-r}{13}$,
∴r=$\frac{65}{18}$,
即⊙O的半径为$\frac{65}{18}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理和相似三角形的判定与性质.

练习册系列答案
相关题目
4.正六边形的周长为12,则该正六边形的内切圆的半径为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
5.方程组$\left\{\begin{array}{l}{x+y=1}\\{3x-y=-5}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ |
 如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )
如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )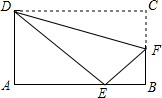 如图,将矩形ABCDE沿DF折叠,使点C落在AB的边上的点E处.
如图,将矩形ABCDE沿DF折叠,使点C落在AB的边上的点E处. )2+
)2+ =0,则∠C的度数为________.
=0,则∠C的度数为________.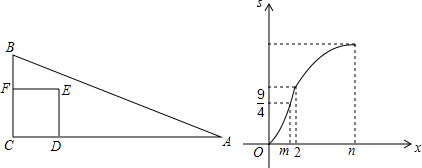
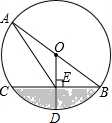 如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.
如图,已知AB是⊙O的直径,半径OD⊥BC于点E,连结AE,$\widehat{CD}$=60°.