题目内容
12.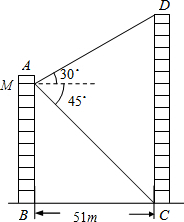 如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)
如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)
分析 过点M作ME⊥CD于E,则四边形BCEP是矩形,得到ME=BC=30,在Rt△MDE中,利用∠DME=30°,求得DE的长;在Rt△MEC中,利用∠EMC=45°,求得CE的长,利用CD=DE﹢CE即可求得结果.
解答 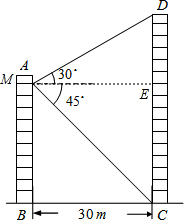 解:过点M作ME⊥CD于E,则四边形BCEM是矩形.
解:过点M作ME⊥CD于E,则四边形BCEM是矩形.
∴ME=BC=51.
在Rt△MDE中,
∵∠DME=30°,ME=30,
∴DE=ME×tan30°=51×$\frac{\sqrt{3}}{3}$=17$\sqrt{3}$.
在Rt△MEC中,∵∠EMC=45°,ME=51,
∴CE=ME×tan45°=51×1=30.
∴CD=DE﹢CE=51﹢17$\sqrt{3}$=30﹢17.3≈80(m).
答:建筑物CD的高约为80m.
点评 本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
7.下列图形中,中心对称图形有( )

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.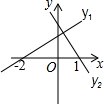 如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )
如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )
 如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )
如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )| A. | x<-2 | B. | -2<x<1 | C. | x>0 | D. | x>1 |
4.正六边形的周长为12,则该正六边形的内切圆的半径为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
1.南水北调中线工程向河南、河北、北京、天津四省市供水,通水后每年可向北方输95亿立方米的水量,基本缓解北方严重缺水局面.95亿立方米用科学记数法表示是( )
| A. | 9.5×106m3 | B. | 9.5×107m3 | C. | 9.5×108m3 | D. | 9.5×109m3 |
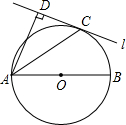 如图,AB为⊙O的直径,AC为弦,过C点的直线为l,AD⊥l于D,又AC平分∠DAB.
如图,AB为⊙O的直径,AC为弦,过C点的直线为l,AD⊥l于D,又AC平分∠DAB. 如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )
如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )