题目内容
10.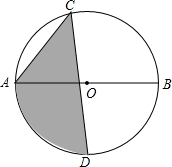 如图,⊙O的直径AB为10,弦AC为6,△ACB的平分线交⊙O于点D,则图中阴影部分的面积为$\frac{17}{2}$+$\frac{25π}{4}$.
如图,⊙O的直径AB为10,弦AC为6,△ACB的平分线交⊙O于点D,则图中阴影部分的面积为$\frac{17}{2}$+$\frac{25π}{4}$.
分析 如图,连接BC、BD、AD、OD,作DN⊥BC于N,DM⊥CA于M,由S四边形ACBD=$\frac{1}{2}$•AC•BC+$\frac{1}{2}$•AD•BD=$\frac{1}{2}$•AC•DM+$\frac{1}{2}$•BC•DN求出DM,再根据S阴=S△ACD+(S扇形OAD-S△AOD)即可解决问题.
解答 解:如图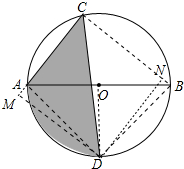 连接BC、BD、AD、OD,作DN⊥BC于N,DM⊥CA于M.
连接BC、BD、AD、OD,作DN⊥BC于N,DM⊥CA于M.
∵AB是直径,AC=6,AB=10,
∴∠ACB=90°,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵CD平分∠ACB,
∴∠DCA=∠DCB=45°,AD=DB,DM=DN,
∵∠ADB=90°,
∴AD2+DB2=AB2,
∴AD=DB=5$\sqrt{2}$,
∵S四边形ACBD=$\frac{1}{2}$•AC•BC+$\frac{1}{2}$•AD•BD=$\frac{1}{2}$•AC•DM+$\frac{1}{2}$•BC•DN,
∴DM=DN=7,
∴S△ACD=$\frac{1}{2}$•AC•DM=21,
∴S阴=S△ACD+(S扇形OAD-S△AOD)=21+$\frac{25π}{4}$-$\frac{25}{2}$=$\frac{17}{2}$+$\frac{25π}{4}$.
故答案为$\frac{17}{2}$+$\frac{25π}{4}$.
点评 本题考查扇形的面积公式、三角形的面积、勾股定理等知识,解题的关键是把不规则图形转化为规则图形解决,学会利用角平分线添加辅助线,属于中考常考题型.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
1.南水北调中线工程向河南、河北、北京、天津四省市供水,通水后每年可向北方输95亿立方米的水量,基本缓解北方严重缺水局面.95亿立方米用科学记数法表示是( )
| A. | 9.5×106m3 | B. | 9.5×107m3 | C. | 9.5×108m3 | D. | 9.5×109m3 |
5.方程组$\left\{\begin{array}{l}{x+y=1}\\{3x-y=-5}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ |
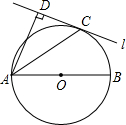 如图,AB为⊙O的直径,AC为弦,过C点的直线为l,AD⊥l于D,又AC平分∠DAB.
如图,AB为⊙O的直径,AC为弦,过C点的直线为l,AD⊥l于D,又AC平分∠DAB.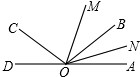 如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=50°,试求∠AOC与∠AOB的度数.
如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=50°,试求∠AOC与∠AOB的度数. 如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )
如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )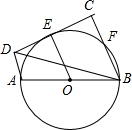 如图,AB是⊙O的直径,CD切⊙O于E,AD⊥CD于点D,BC⊥CD于交⊙O于F,且BF=CF,若AB=6.求BD的长.
如图,AB是⊙O的直径,CD切⊙O于E,AD⊥CD于点D,BC⊥CD于交⊙O于F,且BF=CF,若AB=6.求BD的长.