题目内容
3.已知抛物线y=ax2+bx+c的顶点坐标为(-1,4),与x轴的两个交点间的距离为6,求此抛物线的函数表达式.分析 先利用抛物线的对称性得到抛物线与x轴的两个交点坐标为(-4,0),(2,0),则可设交点式y=a(x+4)(x-2),然后把顶点坐标代入求出a的值即可.
解答 解:∵抛物线y=ax2+bx+c的顶点坐标为(-1,4),
∴抛物线的对称轴为直线x=-1,
∵抛物线与x轴的两个交点间的距离为6,
∴抛物线与x轴的两个交点坐标为(-4,0),(2,0),
设抛物线解析式为y=a(x+4)(x-2),
把(-1,4)代入得a•3•(-3)=4,解得a=-$\frac{4}{9}$,
∴抛物线解析式为y=-$\frac{4}{9}$(x+4)(x-2),即y=-$\frac{4}{9}$x2-$\frac{8}{9}$x+$\frac{32}{9}$.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
11.把正整数1,2,3,4,5,6…按某种规律填入表.
按照这种规律连续填写,2014出现在第1行第1511列.
| 2 | 6 | 10 | 14 | ||||||||
| 1 | 4 | 5 | 8 | 9 | 12 | 13 | … | ||||
| 3 | 7 | 11 | 15 |
12.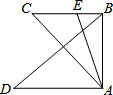 如图AB⊥AD,AB⊥BC,则以AB为一条高线的三角形共有( )个.
如图AB⊥AD,AB⊥BC,则以AB为一条高线的三角形共有( )个.
 如图AB⊥AD,AB⊥BC,则以AB为一条高线的三角形共有( )个.
如图AB⊥AD,AB⊥BC,则以AB为一条高线的三角形共有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |