题目内容
13.在关于x的方程${(x-\sqrt{3})^2}$=m中,对m任取一个数值,使得该方程没有实数根,那么m的值可以是-1.(只需写出一个即可)分析 根据任何一个数的平方都是非负数得出m≥0,得出该方程没有实数根时,m<0任取一个负数即可.
解答 解:在关于x的方程${(x-\sqrt{3})^2}$=m中,对m任取一个数值,使得该方程没有实数根,那么m的值可以是-1.
故答案为-1.
点评 本题考查了解一元二次方程-直接开平方法.用直接开方法求一元二次方程的解的类型有:x2=a(a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).
法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”.

练习册系列答案
相关题目
1.下列不是二次函数关系式的是( )
| A. | y=3x2+4 | B. | y=-$\frac{1}{3}{x^2}$ | C. | y=(x+1)(x-2) | D. | y=$\sqrt{x^2}$ |
8.方程x2-4x-4=0进行配方后,得到的方程是( )
| A. | (x-2)2=8 | B. | (x+2)2=8 | C. | (x-2)2=0 | D. | (x+2)2=16 |
18.若反比例函数y=$\frac{k-1}{x}$的图象位于第一、三象限,则k的取值可以是( )
| A. | 2 | B. | 1 | C. | 0 | D. | 以上都不可以 |
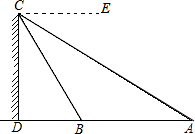 如图,A、B两点与建筑物底部D在同一直线上,从建筑物顶部C点测得∠ECA=30°,∠ECB=60°,且AB=20,求建筑物CD的高.
如图,A、B两点与建筑物底部D在同一直线上,从建筑物顶部C点测得∠ECA=30°,∠ECB=60°,且AB=20,求建筑物CD的高.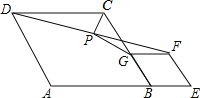 如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则$\frac{CP}{CG}$=$\frac{1}{2}$.
如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则$\frac{CP}{CG}$=$\frac{1}{2}$.