题目内容
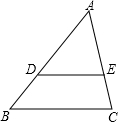 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则
如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则| DE |
| BC |
考点:相似三角形的判定与性质
专题:
分析:由AD=3,DB=2,即可求得AB的长,又由DE∥BC,根据平行线分线段成比例定理,可得DE:BC=AD:AB,则可求得答案.
解答:解:∵AD=4,DB=2,
∴AB=AD+BD=4+2=6,
∵DE∥BC,
△ADE∽△ABC,∴
=
=
=
,
故答案为:
.
∴AB=AD+BD=4+2=6,
∵DE∥BC,
△ADE∽△ABC,∴
| AD |
| AB |
| DE |
| BC |
| 4 |
| 6 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:此题考查了平行线分线段成比例定理.此题比较简单,注意掌握比例线段的对应关系是解此题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
下列命题中,是真命题的是( )
| A、任一多边形的外角中最多有三个是钝角 |
| B、三角形的一个外角等于两个内角的和 |
| C、两直线被第三条直线所截,同位角相等 |
| D、连接平面上三点构成的图形是三角形 |
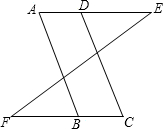 如图,在:①AB∥CD;②AD∥BC;③∠A=∠C中,请你选取其中的两个作为条件,另一个作为结论,写出一个正确命题,并证明其正确性.
如图,在:①AB∥CD;②AD∥BC;③∠A=∠C中,请你选取其中的两个作为条件,另一个作为结论,写出一个正确命题,并证明其正确性. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则∠A的余角是
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则∠A的余角是 如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=5cm,BC=4cm,则点D到直线AB的距离是
如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BD=5cm,BC=4cm,则点D到直线AB的距离是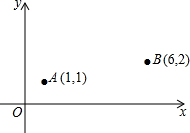 已知A(1,1),B(6,2),C、D分别为x轴、y轴上的动点,在运动的过程中,如果C、D满足|AC-BC|最大,而使|AD+BD|最小,则CD的长为
已知A(1,1),B(6,2),C、D分别为x轴、y轴上的动点,在运动的过程中,如果C、D满足|AC-BC|最大,而使|AD+BD|最小,则CD的长为