题目内容
观察下面的式子:
13=1,1=1,
13+23=9,1+2=3,
13+23+33=36,1+2+3=6,
13+23+33+43=100,1+2+3+4=10,
┅┅
(1)猜一猜13+23+33+43+53等于什么?
(1)猜一猜13+23+33+…+n3等于什么?
(2)写出13+23+33+43+53+63+73+83+93+103的值.
13=1,1=1,
13+23=9,1+2=3,
13+23+33=36,1+2+3=6,
13+23+33+43=100,1+2+3+4=10,
┅┅
(1)猜一猜13+23+33+43+53等于什么?
(1)猜一猜13+23+33+…+n3等于什么?
(2)写出13+23+33+43+53+63+73+83+93+103的值.
考点:规律型:数字的变化类
专题:
分析:观察发现,等式的左边是连续整数的立方和;右边是连续整数的和的平方.
(1)由于1+2+3+4+5=15,所以13+23+33+43+53=152;
(2)由于1+2+3+4+…+n=
n(n+1),所以13+23+33+…+n3=[
n(n+1)]2;
(3)由于1+2+3+4+5+6+7+8+9+10=55,所以13+23+33+43+53+63+73+83+93+103=552.
(1)由于1+2+3+4+5=15,所以13+23+33+43+53=152;
(2)由于1+2+3+4+…+n=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由于1+2+3+4+5+6+7+8+9+10=55,所以13+23+33+43+53+63+73+83+93+103=552.
解答:解:由题意,可得
(1)13+23+33+43+53=(1+2+3+4+5)2=152=225;
(2)13+23+33+…+n3=(1+2+3+4+…+n)2=[
n(n+1)]2;
(3)13+23+33+43+53+63+73+83+93+103=(1+2+3+4+5+6+7+8+9+10)2=552=3025.
(1)13+23+33+43+53=(1+2+3+4+5)2=152=225;
(2)13+23+33+…+n3=(1+2+3+4+…+n)2=[
| 1 |
| 2 |
(3)13+23+33+43+53+63+73+83+93+103=(1+2+3+4+5+6+7+8+9+10)2=552=3025.
点评:本题考查了规律型:数字的变化类,难度适中.注意找等式的规律时,要观察等式的左边和右边的规律,还要注意观察等式的左右两边之间的关系.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图,∠AED=∠ACB,∠DEB=∠GFC,BE⊥AC,求证:FG⊥AC.
如图,∠AED=∠ACB,∠DEB=∠GFC,BE⊥AC,求证:FG⊥AC. 某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.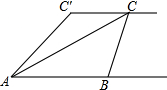 如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 米.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.
如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 米.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.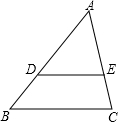 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则
如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则