题目内容
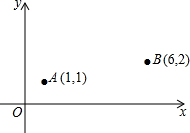 已知A(1,1),B(6,2),C、D分别为x轴、y轴上的动点,在运动的过程中,如果C、D满足|AC-BC|最大,而使|AD+BD|最小,则CD的长为
已知A(1,1),B(6,2),C、D分别为x轴、y轴上的动点,在运动的过程中,如果C、D满足|AC-BC|最大,而使|AD+BD|最小,则CD的长为考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:连接AB,并延长BA交x轴点C,作点B关于y轴的对称点B′,连接B′A交y轴于点D,利用三角形两边之差小于第三边,可得此时|AC-BC|最大,利用轴对称最短路径求法,可得此时|AD+BD|最小,分别求出AB所在的直线,B′A所在的直线,求出C和D的坐标,利用勾股定理求出CD的长.
解答:
解:连接AB,并延长BA交x轴点C,作点B关于y轴的对称点B′,连接B′A交y轴于点D,
利用三角形两边之差小于第三边,可得此时|AC-BC|最大,利用轴对称最短路径求法,可得此时|AD+BD|最小,
设AB所在的直线为:y=kx+b,
∵A(1,1),B(6,2),
∴y=
x+
,
∴C的坐标为(-4,0)
设B′A所在的直线为:y=mx+n,
∵B′(-6,2),A(1,1),
∴y=-
x+
,
D的坐标为(0,
)
∴CD=
=
=
.
故答案为:
.

解:连接AB,并延长BA交x轴点C,作点B关于y轴的对称点B′,连接B′A交y轴于点D,
利用三角形两边之差小于第三边,可得此时|AC-BC|最大,利用轴对称最短路径求法,可得此时|AD+BD|最小,
设AB所在的直线为:y=kx+b,
∵A(1,1),B(6,2),
∴y=
| 1 |
| 5 |
| 4 |
| 5 |
∴C的坐标为(-4,0)
设B′A所在的直线为:y=mx+n,
∵B′(-6,2),A(1,1),
∴y=-
| 1 |
| 7 |
| 8 |
| 7 |
D的坐标为(0,
| 8 |
| 7 |
∴CD=
| CO2+DO2 |
42+(
|
4
| ||
| 7 |
故答案为:
4
| ||
| 7 |
点评:此题主要考查了利用轴对称求最短路径问题和坐标与图形的性质,利用三角形两边之差小于第三边和利用轴对称最短路径求法正确作出图是解题关键.

练习册系列答案
相关题目
若不等式组2<x<a的整数解恰有3个,则a的取值范围是( )
| A、a>5 | B、5<a<6 |
| C、5≤a<6 | D、5<a≤6 |
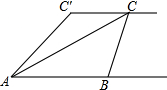 如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 米.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.
如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100 米.当气球沿与BA平行地飘移10秒后到达C′处时,在A处测得气球的仰角为45°.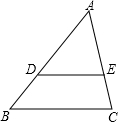 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则
如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则 在方格纸上,每个小格的顶点叫格点,以格点为顶点的三角形叫格点三角形.如图,在4×4的方格纸上,以AB为边的格点三角形ABC的面积为2个平方单位,则符合条件的C点共有
在方格纸上,每个小格的顶点叫格点,以格点为顶点的三角形叫格点三角形.如图,在4×4的方格纸上,以AB为边的格点三角形ABC的面积为2个平方单位,则符合条件的C点共有 如图,AD∥BC,∠A是∠ABC的2倍,
如图,AD∥BC,∠A是∠ABC的2倍,