题目内容
分解因式：
（1）-5a2+25a；
（2）（a2+ab+b2）2-9a2b2．
（1）-5a2+25a；
（2）（a2+ab+b2）2-9a2b2．
考点：提公因式法与公式法的综合运用
专题：
分析：（1）提取公因式-5a整理即可；
（2）先利用平方差公式分解因式，再利用完全平方公式继续分解因式即可．
（2）先利用平方差公式分解因式，再利用完全平方公式继续分解因式即可．
解答：解：（1）-5a2+25a=-5a（a-5）；
（2）（a2+ab+b2）2-9a2b2，
=（a2+ab+b2+3ab）（a2+ab+b2-3ab），
=（a2+4ab+b2）（a2-2ab+b2），
=（a2+4ab+b2）（a-b）2．
（2）（a2+ab+b2）2-9a2b2，
=（a2+ab+b2+3ab）（a2+ab+b2-3ab），
=（a2+4ab+b2）（a2-2ab+b2），
=（a2+4ab+b2）（a-b）2．
点评：本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．
练习册系列答案
阅读快车系列答案
相关题目
如图，∠AED=∠ACB，∠DEB=∠GFC，BE⊥AC，求证：FG⊥AC．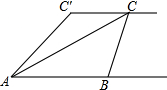
如图，小敏、小亮从A，B两地观测空中C处一个气球，分别测得仰角为30°和60°，A，B两地相距100 米．当气球沿与BA平行地飘移10秒后到达C′处时，在A处测得气球的仰角为45°．
如图，点O和△ABC的三个顶点都在方格图的格点上，请画出△A′B′C′，使△A′B′C′和△ABC关于点O成中心对称．
如图，抛物线y=-x2+2x+3与x轴相交于A、B两点，与y轴交于点C，顶点为D，抛物线的对称轴DF与BC相交于点E，与x轴相交于点F．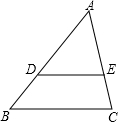
如图，在△ABC中，点D、E分别在AB、AC上，DE∥BC．若AD=4，DB=2，则
在方格纸上，每个小格的顶点叫格点，以格点为顶点的三角形叫格点三角形．如图，在4×4的方格纸上，以AB为边的格点三角形ABC的面积为2个平方单位，则符合条件的C点共有