题目内容
在平面直角坐标系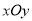 中,抛物线
中,抛物线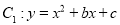 经过点
经过点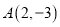 ,且与
,且与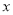 轴的一个交点为
轴的一个交点为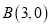 .
.
(1)求抛物线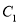 的表达式;
的表达式;
(2)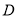 是抛物线
是抛物线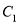 与
与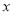 轴的另一个交点,点
轴的另一个交点,点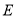 的坐标为
的坐标为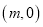 ,其中
,其中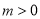 ,△
,△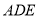 的面积为
的面积为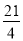 .
.
①求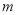 的值;
的值;
②将抛物线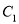 向上平移
向上平移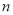 个单位,得到抛物线
个单位,得到抛物线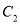 .若当
.若当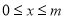 时,抛物线
时,抛物线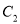 与
与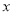 轴只有一个公共点,结合函数的图象,求
轴只有一个公共点,结合函数的图象,求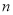 的取值范围.
的取值范围.
练习册系列答案
相关题目
题目内容
在平面直角坐标系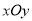 中,抛物线
中,抛物线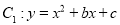 经过点
经过点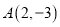 ,且与
,且与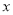 轴的一个交点为
轴的一个交点为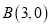 .
.
(1)求抛物线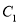 的表达式;
的表达式;
(2)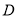 是抛物线
是抛物线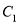 与
与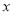 轴的另一个交点,点
轴的另一个交点,点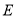 的坐标为
的坐标为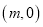 ,其中
,其中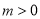 ,△
,△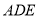 的面积为
的面积为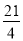 .
.
①求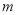 的值;
的值;
②将抛物线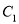 向上平移
向上平移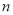 个单位,得到抛物线
个单位,得到抛物线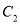 .若当
.若当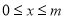 时,抛物线
时,抛物线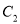 与
与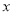 轴只有一个公共点,结合函数的图象,求
轴只有一个公共点,结合函数的图象,求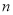 的取值范围.
的取值范围.