题目内容
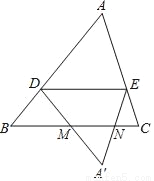
如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.
(1)求证:DB=DM.
(2)若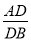 =2,DE=6,求线段MN的长.
=2,DE=6,求线段MN的长.
(3)若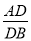 =n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
=n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
练习册系列答案
相关题目
题目内容
如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.
(1)求证:DB=DM.
(2)若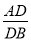 =2,DE=6,求线段MN的长.
=2,DE=6,求线段MN的长.
(3)若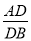 =n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
=n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
