题目内容
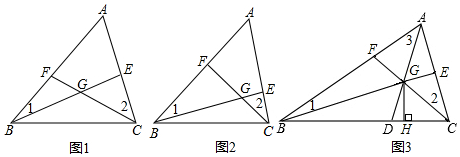
7.在△ABC中,(1)如图1,点E,F分别是AC,AB上一点,若BE,CF相交于点G,请说明∠BGC=∠1+∠A+∠2;
(2)如图2,若BE,CF分别是AC,AB上的高,请说明∠1=∠2理由;
(3)如图3,若∠ABC,∠ACB,∠BAC的角平分线BE,CF,AD相交于点G,则:
①∠1+∠2+∠3=90°;
②若过点G作GH⊥BC于点H,发现∠BGD=∠CGH,请说明理由.
分析 (1)根据三角形的外角性质,求得∠BGC=∠BGP+∠CGP,据此进行计算即可;
(2)根据BE,CF分别是AC,AB上的高,可得△ABE和△ACF是直角三角形,进而得出∠1+∠A=∠2+∠A=90°,据此可得∠1=∠2;
(3)根据∠ABC,∠ACB,∠BAC的角平分线BE,CF,AD相交于点G,可得∠1+∠2+∠3=$\frac{1}{2}$(∠ABC+∠ACB+∠BAC),据此进行计算即可;②根据∠BGD是△ABG的外角,得出∠BGD=∠1+∠3=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠BAC=90°-$\frac{1}{2}$∠ACB,再根据CF平分∠ACB,GH⊥BC,可得Rt△CHG中,∠CGH=90°-∠GCH=90°-$\frac{1}{2}$∠ACB,进而得到∠BGD=∠CGH.
解答 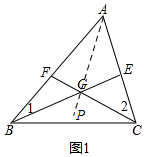 解:(1)∵如图1,连接AG并延长至P,
解:(1)∵如图1,连接AG并延长至P,
∵∠BGP是△ABG的外角,
∴∠BGP=∠1+∠BAP,
同理可得,∠CGP=∠2+∠CAP,
∴∠BGC=∠BGP+∠CGP=∠1+∠BAP+∠2+∠CAP=∠1+∠A+∠2;
(2)∵如图2,BE,CF分别是AC,AB上的高,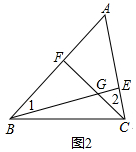
∴△ABE和△ACF是直角三角形,
∴∠1+∠A=∠2+∠A=90°,
∴∠1=∠2;
(3)①如图3,∵∠ABC,∠ACB,∠BAC的角平分线BE,CF,AD相交于点G,
∴∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACB,∠3=$\frac{1}{2}$∠BAC,
∴∠1+∠2+∠3=$\frac{1}{2}$(∠ABC+∠ACB+∠BAC)=$\frac{1}{2}$×180°=90°,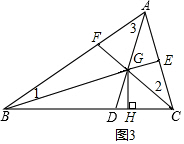
故答案为:90°;
②∵∠BGD是△ABG的外角,
∴∠BGD=∠1+∠3=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠BAC
=$\frac{1}{2}$(180°-∠ACB)=90°-$\frac{1}{2}$∠ACB,
∵CF平分∠ACB,
∴∠GCH=$\frac{1}{2}$∠ACB,
∵GH⊥BC,
∴Rt△CHG中,∠CGH=90°-∠GCH=90°-$\frac{1}{2}$∠ACB,
∴∠BGD=∠CGH.
点评 本题主要考查了三角形内角和定理以及角平分线的定义的运用,解决问题的关键是掌握:三角形内角和等于180°.解决第(3)问的难点在于将∠BGD和∠CGH都用90°-$\frac{1}{2}$∠ACB表示出来.

| A. | m | B. | -my | C. | -y | D. | my |
| A. | M>N | B. | M<N | C. | M=N | D. | 无法确定 |
| A. | x2+4=4x | B. | x2-x-1=0 | C. | 2x2+4x+3=0 | D. | 3x-8=0 |
| A. | 2cm | B. | 3cm | C. | 9cm | D. | 10cm |
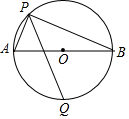 如图,AB为?O的直径,点P在?O上,AP=6,AB=10,PQ平分∠APB,则PQ=$\frac{97\sqrt{2}}{15}$.
如图,AB为?O的直径,点P在?O上,AP=6,AB=10,PQ平分∠APB,则PQ=$\frac{97\sqrt{2}}{15}$.