题目内容
7.解下列不等式组:(1)$\left\{\begin{array}{l}{2x+5>3(x-1)}\\{4x>\frac{x+7}{2}}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x-2≤0}\\{2(x-1)+(3-x)>0}\end{array}\right.$.
分析 (1)根据解不等式组的方法可以求出此不等式组的解集;
(2)根据解不等式组的方法可以求出此不等式组的解集.
解答 解:(1)$\left\{\begin{array}{l}{2x+5>3(x-1)}&{①}\\{4x>\frac{x+7}{2}}&{②}\end{array}\right.$,
解不等式①,得
x<8,
解不等式②,得
x>1,
由①②可得,不等式组的解集是:1<x<8;
(2)$\left\{\begin{array}{l}{x-2≤0}&{①}\\{2(x-1)+(3-x)>0}&{②}\end{array}\right.$,
解不等式①,得
x≤2,
解不等式②,得
x>-1,
由①②可得,不等式组的解集是:-1<x≤2.
点评 本题考查解一元一次不等式组,解答此类问题的关键是明确解一元一次不等式的方法,注意最后写出不等式组的解集.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
18.在“石头、剪子、布”的游戏中,当你出“石头”时,对手与你打平的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
10.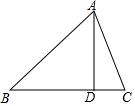 如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )
如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )
 如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )
如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )| A. | $2\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $3\sqrt{2}$ |
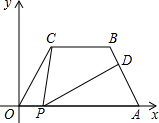 如图所示,在平面直角坐标系中,四边形OABC中BC∥OA,∠COP=∠BAO=60°,OC=AB=4,OA=7,点P为x轴上一个动点,点P不与点O、点A重合.连接CP,过点P作PD交AB于点D.
如图所示,在平面直角坐标系中,四边形OABC中BC∥OA,∠COP=∠BAO=60°,OC=AB=4,OA=7,点P为x轴上一个动点,点P不与点O、点A重合.连接CP,过点P作PD交AB于点D. 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,∠ABD与∠C互补.
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,∠ABD与∠C互补.