题目内容
6.甲、乙两人解答化简求值题:$\frac{1}{a}$+$\sqrt{\frac{1}{{a}^{2}+{a}^{2}-2}}$,其中a=$\frac{1}{3}$,其解法如下:甲:原式=$\frac{1}{a}$+$\sqrt{(\frac{1}{a}-a)^{2}}$=$\frac{1}{a}$+$\frac{1}{a}$-a=$\frac{2}{a}$-a=$\frac{17}{3}$
乙:原式=$\frac{1}{a}$+$\sqrt{(a-\frac{1}{a})^{2}}$=$\frac{1}{a}$+a-$\frac{1}{a}$=a=$\frac{1}{3}$.
请问:谁的解答是错误的?错误原因是什么?
分析 根据二次根式的性质$\sqrt{{a}^{2}}$=|a|可知乙的解答是错误.
解答 解:乙的解答是错误的,
理由如下:
当a=$\frac{1}{3}$时,a-$\frac{1}{a}$<0,
∴$\sqrt{(a-\frac{1}{a})^{2}}$=$\frac{1}{a}$-a.
点评 本题主要考查二次根式的化简求值,熟练掌握二次根式的性质$\sqrt{{a}^{2}}$=|a|是解题的关键.

练习册系列答案
相关题目
18.在“石头、剪子、布”的游戏中,当你出“石头”时,对手与你打平的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
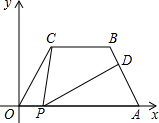 如图所示,在平面直角坐标系中,四边形OABC中BC∥OA,∠COP=∠BAO=60°,OC=AB=4,OA=7,点P为x轴上一个动点,点P不与点O、点A重合.连接CP,过点P作PD交AB于点D.
如图所示,在平面直角坐标系中,四边形OABC中BC∥OA,∠COP=∠BAO=60°,OC=AB=4,OA=7,点P为x轴上一个动点,点P不与点O、点A重合.连接CP,过点P作PD交AB于点D.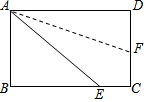 如图,矩形ABCD沿AF折叠,使点D落在BC边上,如果∠BAE=50°,则∠DAF=20°..
如图,矩形ABCD沿AF折叠,使点D落在BC边上,如果∠BAE=50°,则∠DAF=20°.. 小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度.
小刚手里有一根长为80cm的木棒,他把木棒垂直放置在地面上(如图所示),此时测出该木棒在太阳光下的影子的长度为60cm,小刚绕木棒与地面的接触点转动该木棒,想尽办法使木棒的影子最长;问:该木棒转到什么位置时影子最长?并求出此时影子的长度.