题目内容
15.解方程:(1)$\left\{\begin{array}{l}{a+b=12}\\{2a+b=20}\end{array}\right.$
(2)$\left\{\begin{array}{l}{2a-b-c=0}\\{a+c=5}\\{3a+b-2c=1}\end{array}\right.$.
分析 (1)根据加减消元法可以解答此方程组;
(2)根据解三元一次方程组的方法可以解答此方程组.
解答 解:(1)$\left\{\begin{array}{l}{a+b=12}&{①}\\{2a+b=20}&{②}\end{array}\right.$,
②-①,得
a=8,
将a=8代入①,得
b=4,
故原方程组的解是$\left\{\begin{array}{l}{a=8}\\{b=4}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2a-b-c=0}&{①}\\{a+c=5}&{②}\\{3a+b-2c=1}&{③}\end{array}\right.$,
①+③,得
5a-3c=1,④
②×3+④,得
8a=16,
解得,a=2,
将a=2代入②,得
c=3,
将a=2,c=3代入①,得
b=1,
故原方程组的解是$\left\{\begin{array}{l}{a=2}\\{b=1}\\{c=3}\end{array}\right.$.
点评 本题考查解三元一次方程组、解二元一次方程组,解答本题的关键是明确解方程组的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.我市4月份某天的最高气温是22℃,最低气温是8℃,那么这天的温差是( )
| A. | 30℃ | B. | 14℃ | C. | -14℃ | D. | 12℃ |
7.在不等式$\frac{2}{3}$x+2>x的解集中,正整数解的个数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
5.书架上放有3本语文书,4本数学书,5本英语书,小明随机地从书架上抽取一本书,恰好抽到数学书的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
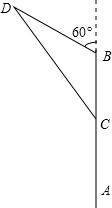 如图,海面上离船A的正北方向100海里处有一船B正以每小时20海里的速度沿北偏西60°的方向行驶,而船A以每小时15海里的速度向正北方向行驶.若两船同时出发,则几小时后两船最近.
如图,海面上离船A的正北方向100海里处有一船B正以每小时20海里的速度沿北偏西60°的方向行驶,而船A以每小时15海里的速度向正北方向行驶.若两船同时出发,则几小时后两船最近.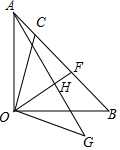 如图,△AOB为等腰直角三角形,∠AOB=90°,C是线段AB上一点,连接OC,作OG⊥OC,且OC=OG,连接AG,取CF=FB,连OF交AG于H,求证:OH⊥AG.
如图,△AOB为等腰直角三角形,∠AOB=90°,C是线段AB上一点,连接OC,作OG⊥OC,且OC=OG,连接AG,取CF=FB,连OF交AG于H,求证:OH⊥AG.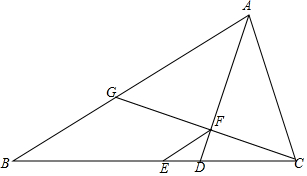 如图,AD是△ABC的平分线,E为BC的中点,EF∥AB交AD于点F,CF的延长线交AB于点G,求证:AG=AC.
如图,AD是△ABC的平分线,E为BC的中点,EF∥AB交AD于点F,CF的延长线交AB于点G,求证:AG=AC.