题目内容
10.小涵将如图1所示学习桌的桌面抽象成了如图2所示的多边形,则图2中∠A+∠B+∠C+∠D+∠E+∠F等于( )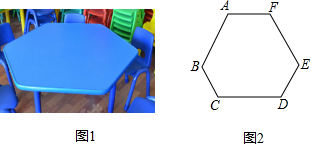
| A. | 640° | B. | 1080° | C. | 900° | D. | 720° |
分析 利用多边形内角和定理,计算六边形的内角和即可.
解答 解:∠A+∠B+∠C+∠D+∠E+∠F=(6-2)×180°=720°.
故选D.
点评 本题考查了多边形的内角与外角:多边形内角和定理为(n-2)•180 (n≥3)且n为整数);多边形的外角和等于360度.

练习册系列答案
相关题目
1. 如图,点E在BC上,点A、E、D在同一条直线上,AB⊥BC,CD⊥BC,若测得BE=20m,EC=10m,CD=20m,则河宽AB=( )
如图,点E在BC上,点A、E、D在同一条直线上,AB⊥BC,CD⊥BC,若测得BE=20m,EC=10m,CD=20m,则河宽AB=( )
 如图,点E在BC上,点A、E、D在同一条直线上,AB⊥BC,CD⊥BC,若测得BE=20m,EC=10m,CD=20m,则河宽AB=( )
如图,点E在BC上,点A、E、D在同一条直线上,AB⊥BC,CD⊥BC,若测得BE=20m,EC=10m,CD=20m,则河宽AB=( )| A. | 60m | B. | 40m | C. | 30m | D. | 20m |
18.下列运算正确的是( )
| A. | $\sqrt{18}$$-\sqrt{2}$=2 | B. | $\sqrt{14}$×$\sqrt{2}$=2$\sqrt{7}$ | C. | ($\sqrt{3}+2)$2=7 | D. | (-2ab2)3=-6a3b6 |
5.书架上放有3本语文书,4本数学书,5本英语书,小明随机地从书架上抽取一本书,恰好抽到数学书的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
15.下列命题是假命题的是( )
| A. | 同位角相等,两直线平行 | |
| B. | 平行于同一直线的两条直线互相平行 | |
| C. | 内错角相等 | |
| D. | 有一个角是60°的等腰三角形是等边三角形 |
2.三角形的重心是( )
| A. | 三条角平分线的交点 | B. | 三边垂直平分线的交点 | ||
| C. | 三条中线的交点 | D. | 三条高所在直线的交点 |
19.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
| A. | 当AB=BC时,它是菱形 | B. | 当AC⊥BD时,它是菱形 | ||
| C. | 当∠ABC=90°时,它是矩形 | D. | 当AC=BD时,它是正方形 |
20.若直线y=3x+m经过第一、三、四象限,则抛物线y=(x-m)2+1的顶点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
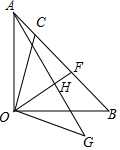 如图,△AOB为等腰直角三角形,∠AOB=90°,C是线段AB上一点,连接OC,作OG⊥OC,且OC=OG,连接AG,取CF=FB,连OF交AG于H,求证:OH⊥AG.
如图,△AOB为等腰直角三角形,∠AOB=90°,C是线段AB上一点,连接OC,作OG⊥OC,且OC=OG,连接AG,取CF=FB,连OF交AG于H,求证:OH⊥AG.