题目内容
19.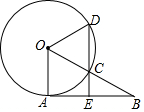 如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3.
如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3.
分析 如图,连接AC,只要证明△ODC是等边三角形,CE是△AOB的中位线即可解决问题.
解答 解:如图,连接AC.
∵AB是切线,
∴OA⊥AB,
∵DC∥OA,OC=CB,
∴AE=EB,DE⊥AB,
∴CA=CB,
∴∠ACE=∠BCE,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠CAE+∠ACE=90°,∠CAE+∠OAC=90°,
∴∠ACE=∠OAC=∠OCA,∵∠BCE=∠OCD,
∴∠OCD=∠OCA=∠ACE=60°,
∴△ODC是等边三角形,
∴CD=OD=2,
∵CE=$\frac{1}{2}$OA=1,
∴DE=CD+CE=2+1=3.
故答案为3.
点评 本题考查切线的性质、平行线等分线段定理、等边三角形的判定和性质、三角形的中位线定理.等腰三角形的性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
10. 在一年一度的国家学生体质测试中,金星中学对全校2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图:
在一年一度的国家学生体质测试中,金星中学对全校2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图:
(1)在这个问题中,总体是什么?
(2)直接写出a,b,c,d的值.
(3)补全频数直方图.
(4)初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″(即260秒)为合格,你能估计出该校初中男生的1000m的合格人数吗?如果能,请求出合格的人数;如果不能,请说明理由.
 在一年一度的国家学生体质测试中,金星中学对全校2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图:
在一年一度的国家学生体质测试中,金星中学对全校2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图:| 序号 | 范围(单位:秒) | 频数 | 频率 |
| 1 | 170<x≤200 | 5 | 0.1 |
| 2 | 200<x≤230 | 13 | a |
| 3 | 230<x≤260 | 15 | 0.3 |
| 4 | 260<x≤290 | c | d |
| 5 | 290<x≤320 | 5 | 0.1 |
| 6 | 320<x≤350 | 2 | 0.04 |
| 7 | 350<x≤380 | 2 | 0.04 |
| 合计 | b | 1.00 |
(2)直接写出a,b,c,d的值.
(3)补全频数直方图.
(4)初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″(即260秒)为合格,你能估计出该校初中男生的1000m的合格人数吗?如果能,请求出合格的人数;如果不能,请说明理由.
8.2016年是雾霾肆虐的一年,河南更是雾霾重灾区,为减少雾霾对人体的伤害,某企业计划购进一批防霾口罩免费发放给学生使用,现甲、乙两个口罩厂有相同的防霾口罩可供选择,其具体销售方案如下:
设购买防霾口罩x个,到两家口罩厂购买所需费用分别为y甲(元),y乙(元).
(1)该企业发现若从两厂分别购买防霾口罩各2500个共花费9750元,若从两厂分别购买防霾口罩各3000个共花费11600元,请求出m,n的值;
(2)分别求出y甲,y乙与x之间的函数关系式;
(3)如果你是该企业的负责人,你认为到哪家口罩厂购买防霾口罩才合算,为什么?
| 甲口罩厂 | |
| 购防霾口罩数量 | 销售单价 |
| 不超过1000个时 | 2元/个 |
| 超过1000个的部分 | m元/个 |
| 乙口罩厂 | |
| 购防霾口罩数量 | 销售单价 |
| 不超过2000个时 | 2元/个 |
| 超过2000个的部分 | n元/个 |
(1)该企业发现若从两厂分别购买防霾口罩各2500个共花费9750元,若从两厂分别购买防霾口罩各3000个共花费11600元,请求出m,n的值;
(2)分别求出y甲,y乙与x之间的函数关系式;
(3)如果你是该企业的负责人,你认为到哪家口罩厂购买防霾口罩才合算,为什么?
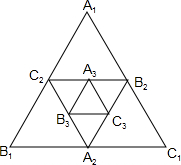 如图,小明作出△A1B1C1,称为第一次操作,分别取△A1B1C1的三边中点A2,B2,C2,作出△A2B2C2,称为第二次操作,用同样的方法,作出△A3B3C3,称为第三次操作,…,第n次操作后,△AnBnCn的面积Sn与△A1B1C1的面积S1之间的数量关系是Sn=$\frac{1}{{4}^{n-1}}$S1.
如图,小明作出△A1B1C1,称为第一次操作,分别取△A1B1C1的三边中点A2,B2,C2,作出△A2B2C2,称为第二次操作,用同样的方法,作出△A3B3C3,称为第三次操作,…,第n次操作后,△AnBnCn的面积Sn与△A1B1C1的面积S1之间的数量关系是Sn=$\frac{1}{{4}^{n-1}}$S1. 已知:如图,△ABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,连接EF.
已知:如图,△ABC中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,连接EF.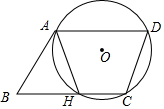 如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H.
如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H. 如图,南湖有一个凉亭A,其正东方向有一棵大树B,一游客想测量A、B之间的距离,他在湖边C处测得A在西南方向,测得B在南偏东33°方向上,且量得B、C之间的距离为50m,求A、B之间的距离(结果精确到0.1m,参考数据:sin33°≈0.545,cos33°≈0.839,tan33°≈0.649)
如图,南湖有一个凉亭A,其正东方向有一棵大树B,一游客想测量A、B之间的距离,他在湖边C处测得A在西南方向,测得B在南偏东33°方向上,且量得B、C之间的距离为50m,求A、B之间的距离(结果精确到0.1m,参考数据:sin33°≈0.545,cos33°≈0.839,tan33°≈0.649)