题目内容
9.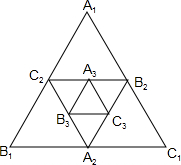 如图,小明作出△A1B1C1,称为第一次操作,分别取△A1B1C1的三边中点A2,B2,C2,作出△A2B2C2,称为第二次操作,用同样的方法,作出△A3B3C3,称为第三次操作,…,第n次操作后,△AnBnCn的面积Sn与△A1B1C1的面积S1之间的数量关系是Sn=$\frac{1}{{4}^{n-1}}$S1.
如图,小明作出△A1B1C1,称为第一次操作,分别取△A1B1C1的三边中点A2,B2,C2,作出△A2B2C2,称为第二次操作,用同样的方法,作出△A3B3C3,称为第三次操作,…,第n次操作后,△AnBnCn的面积Sn与△A1B1C1的面积S1之间的数量关系是Sn=$\frac{1}{{4}^{n-1}}$S1.
分析 根据三角形中位线定理和相似三角形的性质得到△A2B2C2∽△A1B1C1,相似比为$\frac{1}{2}$,S2=$\frac{1}{4}$S1,根据规律解答.
解答 解:∵点A2,B2,C2是△A1B1C1的三边中点,
∴B2C2=$\frac{1}{2}$B1C1,
同理A2C2=$\frac{1}{2}$A1C1,B2A2=$\frac{1}{2}$B1A1,
∴△A2B2C2∽△A1B1C1,相似比为$\frac{1}{2}$,
∴S2=$\frac{1}{4}$S1,
∴S3=$\frac{1}{4}$S2,
∴S3=$\frac{1}{{4}^{2}}$S1,
则Sn=$\frac{1}{{4}^{n-1}}$S1,
故答案为:Sn=$\frac{1}{{4}^{n-1}}$S1.
点评 本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
1.据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338600000亿次,数字338600000用科学记数法可表示为( )
| A. | 3.386×109 | B. | 0.3386×109 | C. | 33.86×107 | D. | 3.386×108 |
 如图,已知AB∥CD,∠A=49°,∠C=29°,则∠E的度数为20°.
如图,已知AB∥CD,∠A=49°,∠C=29°,则∠E的度数为20°.
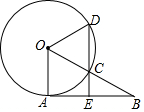 如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3.
如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3.