题目内容
4. 如图,南湖有一个凉亭A,其正东方向有一棵大树B,一游客想测量A、B之间的距离,他在湖边C处测得A在西南方向,测得B在南偏东33°方向上,且量得B、C之间的距离为50m,求A、B之间的距离(结果精确到0.1m,参考数据:sin33°≈0.545,cos33°≈0.839,tan33°≈0.649)
如图,南湖有一个凉亭A,其正东方向有一棵大树B,一游客想测量A、B之间的距离,他在湖边C处测得A在西南方向,测得B在南偏东33°方向上,且量得B、C之间的距离为50m,求A、B之间的距离(结果精确到0.1m,参考数据:sin33°≈0.545,cos33°≈0.839,tan33°≈0.649)
分析 过点C⊥AB于点D,在Rt△BCD中,求出BD、CD的值,然后在Rt△ACD中求出AD的长度,进而可求得AB的长度.
解答  解:过点C⊥AB于点D,
解:过点C⊥AB于点D,
在Rt△BCD中,∵∠BDC=90°,sin33°=$\frac{BD}{BC}$,
∴BD=50×sin33°≈27.25,
∵cos33°=$\frac{CD}{BC}$,
∴CD=50×cos33°≈41.95,
∵∠ACD=45°,
∴AD=CD=41.95,
∴AB=AD+BD=41.95+27.25≈69.2(m).
答:A、B之间的距离约为69.2米.
点评 本题考查了直角三角形的应用,解答本题的关键是根据方向角构造直角三角形,利用三角函数解直角三角形.

练习册系列答案
相关题目
9.若关于x的分式方程$\frac{2}{x-3}$+$\frac{x+m}{3-x}$=2-$\frac{2}{x-3}$有增根,则m的值是( )
| A. | m=1 | B. | m=0 | C. | m=3 | D. | m=0或m=3 |
13. 如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )
如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )
 如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )
如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )| A. | $\frac{π}{2}$-1 | B. | 2π-2 | C. | π+1 | D. | 2π-4 |
 如图,AB为半⊙O的直径,CA与半圆O相切,四边形BOCD是平行四边形,BD与半⊙O交于点E
如图,AB为半⊙O的直径,CA与半圆O相切,四边形BOCD是平行四边形,BD与半⊙O交于点E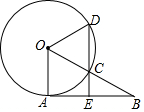 如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3.
如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3.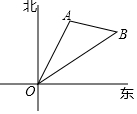 如图,海岛A在灯塔O处北偏东25°,海岛B在灯塔O处北偏东55°,海岛A在海岛B的北偏西80°,已知海岛A到灯塔的距离为80海里,求海岛B到灯塔的距离.(结果保留根号)
如图,海岛A在灯塔O处北偏东25°,海岛B在灯塔O处北偏东55°,海岛A在海岛B的北偏西80°,已知海岛A到灯塔的距离为80海里,求海岛B到灯塔的距离.(结果保留根号)