题目内容
14.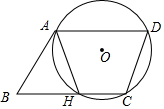 如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H.
如图,⊙O过?ABCD的顶点A,D,C,边AB与⊙O相切于点A,边BC与⊙O相交于点H.(1)求证:AB=AH;
(2)若AB=2,AD=$\sqrt{17}$,求sin∠BAH的值.
分析 (1)根据圆内接四边形可知:∠AHB=∠D,由平行四边形的性质可知:∠B=∠D,从而可证明AB=AH.
(2)连接OA并延长OA交CD于E,交⊙O于点F,连接HF,由垂径定理可求出DE=1,由勾股定理可求AE,从而可求出AF的长度,易证∠BAH=∠F,从而可知sin∠BAH=$\frac{AH}{AF}$.
解答 解:(1)圆内接四边形可知:∠AHB=∠D,
由平行四边形的性质可知:∠B=∠D,
∴∠AHB=∠B,
∴AB=AH
(2)连接OA并延长OA交CD于E,交⊙O于点F,连接HF,
∵AB是⊙O的切线,
∴∠BAE=90°,
∵AB∥CD,AB=CD=2,
∴∠AED=90°,
由垂径定理可知:DE=$\frac{1}{2}$CD=1,
∴由勾股定理可知:AE=4,
连接OD
设OA=OD=r,
∴OE=4-r,
在Rt△ODE中,
∴r2=(4-r)2+1,
解得:r=$\frac{17}{8}$,
∴AF=2r=$\frac{17}{4}$,
∵AF是⊙O的直径,
∴∠BAH+∠FAH=∠F+∠FAH=90°,
∴∠BAH=∠F,
∵AB=AH=2,
∴sin∠BAH=sin∠F=$\frac{AH}{AF}$=$\frac{2}{\frac{17}{4}}$=$\frac{8}{17}$
点评 本题考查圆的综合问题,解题的关键是构造辅助线,利用垂径定理以及勾股定理求解,本题属于中等题型.

练习册系列答案
相关题目
3.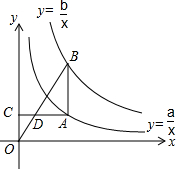 如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
 如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )| A. | a+b=4 | B. | a+b=3 | C. | 3a-b=0 | D. | 2a-b=0 |
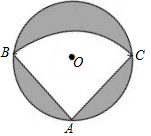 有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.
有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.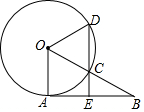 如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3.
如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3.
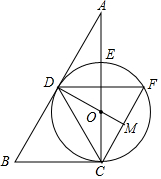 如图,在△ABC中,点O在边AC上,⊙O与△ABC的边AC,AB分别切于C、D两点,与边AC交于点E,弦$\widehat{CF}$与AB平行,与DO的延长线交于M点.
如图,在△ABC中,点O在边AC上,⊙O与△ABC的边AC,AB分别切于C、D两点,与边AC交于点E,弦$\widehat{CF}$与AB平行,与DO的延长线交于M点.