题目内容
11.已知$\left\{\begin{array}{l}{x=0}\\{y=-\frac{1}{2}}\end{array}\right.$是方程组$\left\{\begin{array}{l}{x-b=y}\\{5x+2a=2y}\end{array}\right.$的解,则代数式a+b的值为0.分析 首先把$\left\{\begin{array}{l}{x=0}\\{y=-\frac{1}{2}}\end{array}\right.$代入关于x、y的方程组$\left\{\begin{array}{l}{x-b=y}\\{5x+2a=2y}\end{array}\right.$可得关于a、b的方程组$\left\{\begin{array}{l}{0-b=-\frac{1}{2}}\\{0+2a=-1}\end{array}\right.$,解方程组可得a、b的值,进而可得代数式a+b的值.
解答 解:把$\left\{\begin{array}{l}{x=0}\\{y=-\frac{1}{2}}\end{array}\right.$代入关于x、y的方程组$\left\{\begin{array}{l}{x-b=y}\\{5x+2a=2y}\end{array}\right.$可得:$\left\{\begin{array}{l}{0-b=-\frac{1}{2}}\\{0+2a=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{1}{2}}\end{array}\right.$,
把$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{1}{2}}\end{array}\right.$代入a+b=-$\frac{1}{2}$+$\frac{1}{2}$=0.
故答案为:0.
点评 此题主要考查了二元一次方程组的解,当遇到有关二元一次方程组的解的问题时,要回到定义中去,通常采用代入法,即将解代入原方程组,这种方法主要用在求方程中的字母系数.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案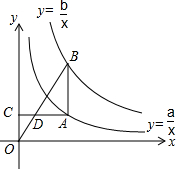 如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )| A. | a+b=4 | B. | a+b=3 | C. | 3a-b=0 | D. | 2a-b=0 |
 如图,已知AB∥CD,∠A=49°,∠C=29°,则∠E的度数为20°.
如图,已知AB∥CD,∠A=49°,∠C=29°,则∠E的度数为20°.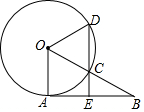 如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3.
如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3.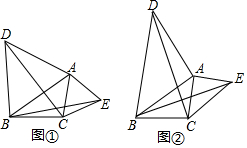
 如图,锐角△ABC内接于⊙O,E为CB延长线上一点,连接AE交⊙O于点D,∠E=∠BAC,连接BD.
如图,锐角△ABC内接于⊙O,E为CB延长线上一点,连接AE交⊙O于点D,∠E=∠BAC,连接BD.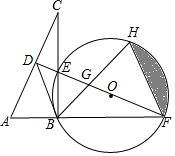 如图所示,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
如图所示,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.