题目内容
8.2016年是雾霾肆虐的一年,河南更是雾霾重灾区,为减少雾霾对人体的伤害,某企业计划购进一批防霾口罩免费发放给学生使用,现甲、乙两个口罩厂有相同的防霾口罩可供选择,其具体销售方案如下:| 甲口罩厂 | |
| 购防霾口罩数量 | 销售单价 |
| 不超过1000个时 | 2元/个 |
| 超过1000个的部分 | m元/个 |
| 乙口罩厂 | |
| 购防霾口罩数量 | 销售单价 |
| 不超过2000个时 | 2元/个 |
| 超过2000个的部分 | n元/个 |
(1)该企业发现若从两厂分别购买防霾口罩各2500个共花费9750元,若从两厂分别购买防霾口罩各3000个共花费11600元,请求出m,n的值;
(2)分别求出y甲,y乙与x之间的函数关系式;
(3)如果你是该企业的负责人,你认为到哪家口罩厂购买防霾口罩才合算,为什么?
分析 (1)根据题目中的数据和表格中的数据可以列出关于m、n的二元一次方程组,从而可以求得m、n的值;
(2)根据(1)中的m、n的值和题意,可以分别求出y甲,y乙与x之间的函数关系式;
(3)根据题意可以分段写出到哪家口罩厂购买防霾口罩才合算,注意要写明理由.
解答 解:(1)由题意可得,
$\left\{\begin{array}{l}{1000×2+(2500-1000)m+2000×2+(2500-2000)n=9750}\\{1000×2+(3000-1000)m+2000×2+(3000-2000)n=11600}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{m=1.9}\\{n=1.8}\end{array}\right.$,
即m的值是1.9,n的值是1.8;
(2)由题意可得,
y甲与x之间的函数关系式是:当0≤x≤1000时,y甲=2x,
当x>1000时,y甲=1000×2+(x-1000)×1.9=1.9x+100,
y乙与x之间的函数关系式是:当0≤x≤2000时,y乙=2x,
当x>2000时,y乙=2000×2+(x-2000)×1.8=1.8x+400,
由上可得,y甲与x之间的函数关系式是:y甲=$\left\{\begin{array}{l}{2x}&{(0≤x≤1000)}\\{1.9x+100}&{(x>1000)}\end{array}\right.$,
y乙与x之间的函数关系式是:y乙=$\left\{\begin{array}{l}{2x}&{(0≤x≤2000)}\\{1.8x+400}&{(x>2000)}\end{array}\right.$;
(3)当0≤x≤1000时,在两家口罩厂购买防霾口罩一样,
当1000<x<3000时,在甲口罩厂购买防霾口罩才合算,
当x=3000时,在两家口罩厂购买防霾口罩一样,
当x>3000时,在乙口罩厂购买防霾口罩才合算,
理由:令1.9x+100=1.8x+400,
解得,x=3000,
∴当0≤x≤1000时,在两家口罩厂购买防霾口罩一样,
当1000<x<3000时,在甲口罩厂购买防霾口罩才合算,
当x=3000时,在两家口罩厂购买防霾口罩一样,
当x>3000时,在乙口罩厂购买防霾口罩才合算.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,求出相应的函数解析式,利用方程的思想、函数的性质解答.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案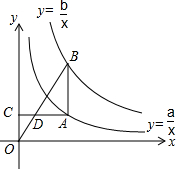 如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )
如图,线段AB平行于y轴,双曲线y=$\frac{a}{x}$(x>0)与y=$\frac{b}{x}$(x>0)分别经过点A,点B,过点A作y轴的垂线段,垂足为C,连结OB,与AC相交于点D,若AD=2DC,则a,b之间的关系是( )| A. | a+b=4 | B. | a+b=3 | C. | 3a-b=0 | D. | 2a-b=0 |
 如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )
如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )| A. | $\frac{π}{2}$-1 | B. | 2π-2 | C. | π+1 | D. | 2π-4 |
| A. | a=3,b=2 | B. | a=-3,b=2 | C. | a=3,b=-2 | D. | a=-3,b=-2 |

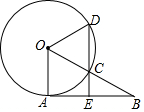 如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3.
如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,过点C作CD∥OA分别交⊙O、AB于点D、E,若点C是OB的中点,且⊙O的半径为2,则DE的长为3. 如图,锐角△ABC内接于⊙O,E为CB延长线上一点,连接AE交⊙O于点D,∠E=∠BAC,连接BD.
如图,锐角△ABC内接于⊙O,E为CB延长线上一点,连接AE交⊙O于点D,∠E=∠BAC,连接BD.