题目内容
14．已知抛物线y=x2+2m-m2，根据下列条件分别求m的值．（1）抛物线过原点．
（2）抛物线的最小值为-3．
分析 （1）直接把原点（0，0）代入抛物线，求出m的值即可；
（2）根据抛物线的解析式判断出其开口方向，进而可得出m的值．
解答 解：（1）∵抛物线y=x2+2m-m2过原点，
∴当x=0时，y=0，即2m-m2=0，解得m=0或m=2；
（2）∵抛物线y=x2+2m-m2，中，a=1＞0，
∴当x=0时，抛物线的值最小，
∴2m-m2=-3，解得m=-1或m=3．
点评 本题考查的是二次函数的性质，熟知二次函数的最值问题是解答此题的关键．
练习册系列答案
相关题目
一副三角尺按如图的位置摆放（顶点C 与F 重合，边CA与边FE叠合，顶点B、C、D在一条直线上）．将三角尺DEF绕着点F按顺时针方向旋转n°后（0＜n＜180 ），如果EF∥AB，那么n的值是45．
10．若a＞b，则下列不等式中，不成立的是（ ）
| A． | $\frac{a}{3}$＞$\frac{b}{3}$ | B． | a-3＞b-3 | C． | ac2＞bc2 | D． | -a＜-b |
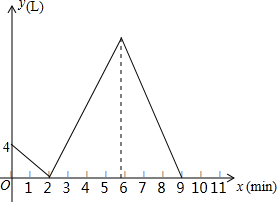某容器装有一个进水管和一个出水管，从某时刻开始2min内既进水又出水，在随后的4min内只进水不出水，之后关闭进水管，打开出水管，容器内的水量y（L）与时间x（min）之间的函数图象如图所示．
19．若点A（a，-2）、B（4，b）在正比例函数y=kx的图象上，则下列等式一定成立的是（ ）
| A． | a-b=6 | B． | a+b=-10 | C． | a•b=-8 | D． | $\frac{a}{b}$=-2 |
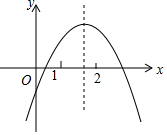二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①2a+b＞0；②abc＜0；③b2-4ac＞0； ④a+b+c＜0；⑤4a-2b+c＞0，其中的正确结论是①③⑤（填写序号）
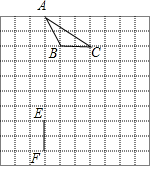如图，在8×8的正方形网格中，△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上．请你在图中找出一点D（仅一个点即可），连结DE，DF，使△DEF与△ABC全等，并给予证明．
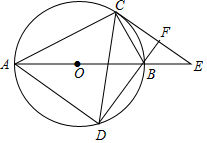如图，四边形ABCD是⊙O的内接四边形，AB为直径，弦CA=CD，AB=5，BD=3，过C作CE⊥DB，垂足为F，交AB的延长线于E．