题目内容
3.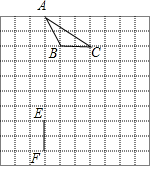 如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上.请你在图中找出一点D(仅一个点即可),连结DE,DF,使△DEF与△ABC全等,并给予证明.
如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上.请你在图中找出一点D(仅一个点即可),连结DE,DF,使△DEF与△ABC全等,并给予证明.
分析 根据题意找到一个格点D,使DE=AB=$\sqrt{2}$、DF=AC=$\sqrt{13}$或DF=AB=$\sqrt{2}$、DE=AC=$\sqrt{13}$,即可根据“SSS”判定俩三角形全等.
解答 解:解法一、如图1或图2的点D,连结DE,DF.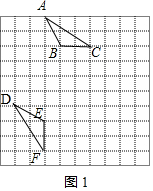
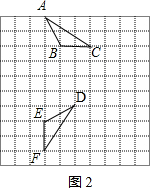
∵在△DEF中,$DE=\sqrt{{2^2}+{1^2}}=\sqrt{5},DF=\sqrt{{3^2}+{2^2}}=\sqrt{13}$,EF=2.
在△ABC中,$AB=\sqrt{{2^2}+{1^2}}=\sqrt{5},AC=\sqrt{{3^2}+{2^2}}=\sqrt{13}$,BC=2.
∴DE=AB,DF=AC,EF=BC.
∴△DEF≌△ABC(SSS).
解法二、如图3或图4的点D,连结DE,DF.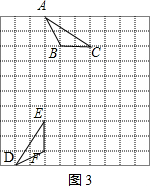
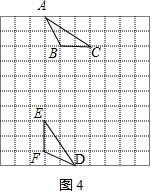
证明:∵在△DEF中,$DF=\sqrt{{2^2}+{1^2}}=\sqrt{5},DE=\sqrt{{3^2}+{2^2}}=\sqrt{13}$,EF=2,
在△ABC中,$AB=\sqrt{{2^2}+{1^2}}=\sqrt{5},AC=\sqrt{{3^2}+{2^2}}=\sqrt{13}$,BC=2.
∴DF=AB,DE=AC,EF=BC.
∴△DFE≌△ABC(SSS).
点评 本题主要考查作图-应用设计作图及全等三角形的判定,熟练掌握勾股定理及全等三角形的判定是解题的关键.

练习册系列答案
相关题目
18.下列式子为最简二次根式的是( )
| A. | $\sqrt{\frac{x}{5}}$ | B. | $\sqrt{8}$ | C. | $\sqrt{3{x}^{2}y}$ | D. | $\sqrt{{x}^{2}-9}$ |
13.若二次函数y=ax2+1的图象经过点(-2,0),则关于x的方程a(x-2)2+1=0的实数根为( )
| A. | x1=0,x2=4 | B. | x1=-2,x2=6 | C. | x1=$\frac{3}{2}$,x2=$\frac{5}{2}$ | D. | x1=-4,x2=0 |
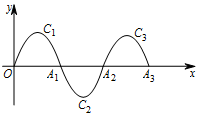 如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )
如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )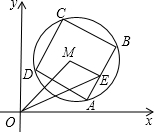 如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.
如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.