题目内容
6.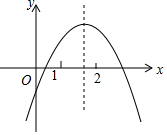 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0; ④a+b+c<0;⑤4a-2b+c>0,其中的正确结论是①③⑤(填写序号)
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0; ④a+b+c<0;⑤4a-2b+c>0,其中的正确结论是①③⑤(填写序号)
分析 由二次函数的开口方向,对称轴x>1,以及二次函数与y的交点在x轴的上方,与x轴有两个交点等条件来判断各结论的正误即可.
解答 解:①∵二次函数的开口向下,∴a<0,对称轴在1的右边,∴-$\frac{b}{2a}$>1,∴2a+b>0,故①正确;
②观察图象,抛物线与y轴的交点在x轴下方,∴c<0,
又∵对称轴为x=-$\frac{b}{2a}$在x轴的正半轴上,故x=-$\frac{b}{2a}$=>0,∵a<0,∴b>0.
∴abc>0,故②错误.
③∵二次函数与x轴有两个交点,∴△=b2-4ac>0,故③正确.
④观察图象,当x=1时,函数值y=a+b+c>0,故④错误;
⑤观察图象,当x=-2时,函数值y=4a-2b+c<0,故⑤正确.
故答案为:①③⑤.
点评 此题主要考查了二次函数的图象与系数的关系,熟练掌握二次函数的性质是解答此题的关键.

练习册系列答案
相关题目
1.下列运算结果正确的是( )
| A. | 3a-a=2 | B. | (a-b)2=a2-b2 | C. | 6ab2÷(-2ab)=-3b | D. | a(a+b)=a2+b |
16.在平面直角坐标系中,点A、B的坐标分别为(2,0),(4,0),点C的坐标为(m,$\sqrt{3}$m)(m为非负数),则CA+CB的最小值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 2$\sqrt{7}$ |
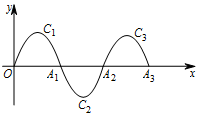 如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )
如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )