题目内容
8.已知数轴上动点A表示整数x的点的位置开始移动,每次移动的规则如下:当点A所在位置表示的数是7的整数倍时,点A向左移动3个单位,否则,点A向右移动1个单位,按此规则,点A移动n次后所在位置表示的数记做xn.例如,当x=1时,x3=4,x6=7,x7=4,x8=5.①若x=1,则x14=7;
②若|x+x1+x2+x3+…+x20|的值最小,则x3=-1.
分析 (1)按照规律写出x14即可.
(2)当x=-3时,|x+x1+x2+x3+…+x20|的值最小,由此可以解决问题.
解答 解:①由题意:x1=2,x2=3,x3=4,x4=5,x5=6,x6=7,x7=4,x8=5,x9=6,x10=7,x11=4,x12=5,x13=6,x14=7.
故答案为x14=7.
②特殊值法:
当x=-6时,可得|x+x1+x2+x3+…+x20|=44,
当x=-5时,可得|x+x1+x2+x3+…+x20|=39,
当x=-4时,可得|x+x1+x2+x3+…+x20|=34,
当x=-3时,可得|x+x1+x2+x3+…+x20|=33,
当x=-2时,可得|x+x1+x2+x3+…+x20|=32,
当x=-1时,可得|x+x1+x2+x3+…+x20|=31,
当x=0时,可得|x+x1+x2+x3+…+x20|=30,
综上所述,x=0时,|x+x1+x2+x3+…+x20|的值最小,此时x3=-1
故答案为-1.
点评 本题考查规律型:图形的变化,解题的关键是连接题意,利用规律解决问题,可以取特殊值尝试一下,找到x为何值时|x+x1+x2+x3+…+x20|的值最小,属于中考常考题型.

练习册系列答案
相关题目
2. 如图,数轴上的A,B,C,D四点中,与表示数$\sqrt{17}$的点数接近的点是( )
如图,数轴上的A,B,C,D四点中,与表示数$\sqrt{17}$的点数接近的点是( )
 如图,数轴上的A,B,C,D四点中,与表示数$\sqrt{17}$的点数接近的点是( )
如图,数轴上的A,B,C,D四点中,与表示数$\sqrt{17}$的点数接近的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
17.下列计算中,正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\root{3}{(-3)^{3}}$=3 | D. | $\sqrt{(3.14-π)^{2}}$=π-3.14 |
18.函数y=$\sqrt{3-x}$+$\frac{1}{x-3}$中自变量x的取值范围是( )
| A. | x≤3 | B. | x<3 | C. | x≠3 | D. | x>3 |
 如图,在同一个平面直角坐标系xOy中,虚半圆O是函数y=$\sqrt{25-{x}^{2}}$(-5≤x≤5)的图象,实曲线(两支)是函数y=$\frac{k}{|x|}$(k≠0)的图象:已知方程$\sqrt{25-{x}^{2}}$=$\frac{k}{|x|}$(k≠0)有一个解为x=-3,则该方程其余的解为3、4、-4.
如图,在同一个平面直角坐标系xOy中,虚半圆O是函数y=$\sqrt{25-{x}^{2}}$(-5≤x≤5)的图象,实曲线(两支)是函数y=$\frac{k}{|x|}$(k≠0)的图象:已知方程$\sqrt{25-{x}^{2}}$=$\frac{k}{|x|}$(k≠0)有一个解为x=-3,则该方程其余的解为3、4、-4. 如图,在△ABC中,AC的垂直平分线交AB于点E,D为垂足,连接EC.若∠A=30°,则∠BEC=60°.
如图,在△ABC中,AC的垂直平分线交AB于点E,D为垂足,连接EC.若∠A=30°,则∠BEC=60°.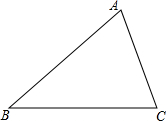 如图,锐角角形ABC中,BC>AB>AC,小骏同学按照下列步骤作图:
如图,锐角角形ABC中,BC>AB>AC,小骏同学按照下列步骤作图: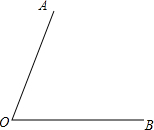 己知∠AOB=70°,根据语句画图,并填空
己知∠AOB=70°,根据语句画图,并填空