题目内容
13.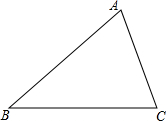 如图,锐角角形ABC中,BC>AB>AC,小骏同学按照下列步骤作图:
如图,锐角角形ABC中,BC>AB>AC,小骏同学按照下列步骤作图:(1)作∠BAC的角平分线AD交BC于D点.
(2)过D作DE∥AB交AC于点E.
根据他画出的图形,请你判断△ADE是什么三角形,并请说明理由.
分析 利用几何语言画出线段AD和DE,则根据角平分线的定义得到∠BAD=∠CAD,再根据平行线的性质得DE∥AC,所以∠EDA=∠CAD,于是根据等腰三角形的判定定理可判定△ADE的形状.
解答 解:如图,△ADE为等腰三角形.
理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠EDA=∠CAD,
∴∠EDA=∠EAD,
∴△ADE为等腰三角形.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
10. 由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )
由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )
 由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )
由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
1.下列式子中,代数式书写规范的是( )
| A. | a•3 | B. | 2ab2c | C. | $\frac{{a}^{2}b}{4}$ | D. | a×b÷c |
2.下列代数运算正确的是( )
| A. | 2-3=-8 | B. | (2x2)3=8x6 | C. | x6÷x2=x3 | D. | x2+x3=2x5 |
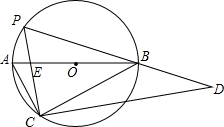 如图,直角△ABC内接于⊙O,∠C=90°,点P在弧AB上移动,P,C分别位于AB的异侧(P不与A,B重合),△PCD也为直角三角形,∠PCD=90°,且直角△PCD的斜边PD经过点B,BA,PC相交于点E.
如图,直角△ABC内接于⊙O,∠C=90°,点P在弧AB上移动,P,C分别位于AB的异侧(P不与A,B重合),△PCD也为直角三角形,∠PCD=90°,且直角△PCD的斜边PD经过点B,BA,PC相交于点E.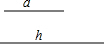 如图,已知两条线段的长度分别为a和h.
如图,已知两条线段的长度分别为a和h.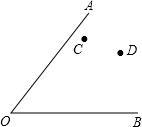 如图所示,点C、D是∠AOB内部的两点.
如图所示,点C、D是∠AOB内部的两点.