Question

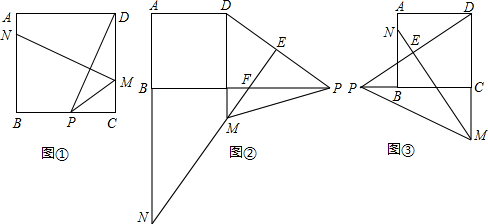
正方形ABCD中，P为直线BC上的一点，DP的垂直平分线交射线DC于M，交DP于E，交射线AB于N．
（1）当点M在CD边上时，如图①，求证：PM-CP=AN；
（2）当点M在边延长线上，如图②、图③的位置时，上述结论是否成立？写出你的猜想，不需要证明．

Answer 1

考点：全等三角形的判定与性质,正方形的性质

专题：

分析：（1）过N作NQ∥AD，则NQ=AD，AN=DQ，易证∠MNQ=∠PDC，即可证明△MNQ≌△PDC，可得QM=PC，再根据垂直平分线性质可得DM=PM，即可解题；
（2）①作MQ∥BF，则AQ=DM，QM=AD=CD，易证∠NMQ=∠MDE，即可证明△NMQ≌△PDC，可得QN=PC，再根据垂直平分线性质可得PM=AQ，即可解题；
③作NQ∥BC，则NQ=AD=CD，AN=DQ，易证∠NMD=∠CPD，即可证明△CDP≌△EDM，可得QM=CP，再根据垂直平分线性质可得DM=PM，即可解题．

解答：证明：（1）过N作NQ∥AD，则NQ=AD，AN=DQ，

∵MN是PD垂直平分线，
∴DM=PM，
∵∠NMQ+∠MNQ=90°，∠NMQ+∠PDC=90°，
∴∠MNQ=∠PDC，
∵在△MNQ和△PDC中，

∠MQN=∠PCD=90° NQ=CD ∠MNQ=∠PDC

，
∴△MNQ≌△PDC，（ASA）
∴QM=PC，
∵DM=DQ+QM，
∴PM=AN+PC，即PM-CP=AN；
（2）①M在图②位置时，不成立，新结论为AN=PM+CP；
理由：作MQ∥BF，则AQ=DM，QM=AD=CD，∠QMD=90°，

∵EF是PD垂直平分线，∴DM=PM，
∴PM=AQ，
∵∠NMQ+∠DME=90°，∠DME+∠MDE=90°，
∴∠NMQ=∠MDE，
∵在△NMQ和△PDC中，

∠NMQ=∠MDE QM=CD ∠MQN=∠DCP=90°

，
∴△NMQ≌△PDC，（ASA）
∴QN=PC，
∵AN=AQ+QN，
∴AN=PM+CP；
②M在图③位置时，成立，
理由：作NQ∥BC，则NQ=AD=CD，AN=DQ，

∵EM是PD的垂直平分线，
∴DM=PM，
∵∠NMD+∠MDE=90°，∠CPD+∠MDE=90°，
∴∠NMD=∠CPD，
∵在△CDP和△EDM中，

∠NMD=∠CPD ∠MQN=∠PCD CD=NQ

，
∴△CDP≌△EDM，（AAS）
∴QM=CP，
∵DM=QM+DQ，
∴PM=AN+CP，即PM-CP=AN．

点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△MNQ≌△PDC、△NMQ≌△PDC和△CDP≌△EDM是解题的关键．